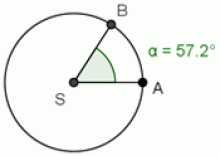
Teorie
Úhel můžeme definovat jako část roviny ohraničené dvěma polopřímkami se společným počátkem. Obě polopřímky pak označujeme jako ramena úhlu a jejich společný bod jako vrchol úhlu. Obě ramena leží v obou úhlech. Každý bod roviny, který neleží na žádném z ramen, je vnitřním bodem jednoho z úhlů. Nejsou-li polopřímky opačné, je jeden úhel menší a nazývá se konvexní úhel, druhý, větší úhel označujeme jako nekonvexní.
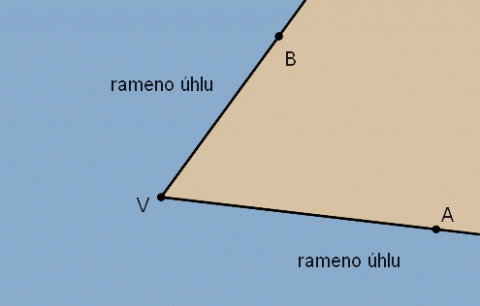
Rozdělení roviny na dva úhly.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.
Podle vzájemné polohy obou polopřímek můžeme rozlišit úhly přímé (obě přímky jsou opačné), nulové (přímky splývají) a plné (přímky splývají).
Na obrázkou jsou stejnou barvou vyznačeny úhly vrcholové a různou barvou úhly vedlejší. Pravý úhel je takový úhel, který je shodný se svým úhlem vedlejším. Všechny pravé úhly jsou shodné.
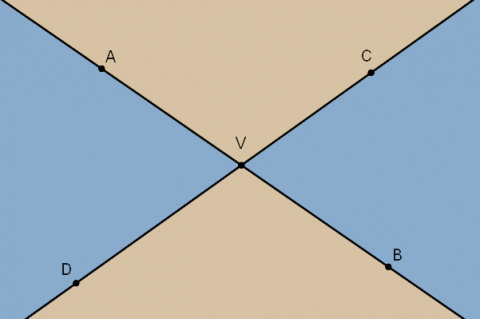
Úhly vedlejší a vrcholové.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.
Podle velikosti úhlu můžeme rozdělit na pravý, ostrý (jeho velikost je menší než pravý) a tupý (jeho velikost je větší než pravý). Je-li velikost vnitřního úhlu α. Velikost úhlu můžeme měřit v různých mírách. Např. v obloukové, stupňové nebo setinné.
Jednotkou stupňové míry je stupeň šedesátinný (označení 1o), který představuje 1/90 pravého úhlu, z úhlového stupně jsou odvozeny úhlová minuta (1´ = 1/60°) a úhlová vteřina (1´´ = 1/60 ´ = 1/3600 °).
Jednotkou oobloukové míry je radián (rad). Jeden radián sestrojíme pomocí kružnice, na které sestrojíme oblouk o stejné délce jako je její poloměr, pak příslušný úhel odpovídá jednomu radiánu.
Pravý úhel je pomocí této jednotky dán jako π/2, úhel plný jako 2π. Pro převod platí následující vztahy:
1 rad = 57° 17´ 44,81´´
360° = 2 π rad
180° = π rad
Jednotkou setinné míry je úhlový stupeň setinný neboli grad (označení 1g), který představuje 1/100 pravého úhlu. Grad se dělí na 100 setinných minut, setinná minuta se dělí na 100 setinných vteřin.
Velkým překvapením pro fyziky a techniky bylo, že tělesa s drsnějším povrchem lépe přidržují mezní vrstvu vzduchu a brání tak vzniku vírů. Proto i míček s drsným povrchem doletí dál, než míček s povrchem hladším. O tom nás přesvědčí i důlkovaný povrch golfového míčku nebo chlupatý povrch tenisového míčku.

Golfový míček.
Zdroj: freedigitalphotos.net. Free picture.