Teorie
Pojem funkce vznikl ze sledování změn a závislostí různých jevů, s nimiž se člověk setkával v denním životě, při studiu přírody atd. Joseph Fourier a Peter Dirichlet dospěli k závěru, že funkci je třeba chápat jako určitou závislost mezi veličinami, bez ohledu na to, zda je k dispozici vzorec tuto závislost vyjadřující. Někdy je jednoduché takovou funkci sestavit. Snadno například můžeme zjistit, jakou dráhu urazí automobil jedoucí známou rychlostí v závislosti na tom, jak dlouho jede. Nebo dokážeme určit přírůstek našich úspor v bance v závislosti na době spoření, pokud známe úrokovou míru a její změny. Jindy je naopak skoro nemožné přijít na to, jak taková funkce vypadá, neboť nemáme dostatek informací o parametrech, které do jejího zápisu vstupují. Třeba takovou závislost teploty ovzduší v daném okamžiku na zeměpisné poloze a nadmořské výšce.
Matematika definuje funkci na množině jako předpis, který každému číslu z množiny A přiřazuje právě jedno reálné číslo. Funkce se značí f, g, h, … a můžeme je zapsat y = f(x). Tento zápis zavedl v roce 1733 Alexis Clairaut. Proměnná x se nazývá nezávisle proměnná (argument) a proměnná y se nazývá závisle proměnná. Reálné číslo y se pro určité reálné číslo x nazývá funkční hodnota funkce f a označuje se f(x). Funkci lze zadat charakteristickou vlastností, výčtem prvků, graficky, funkčním předpisem apod. Každé uspořádané dvojici x, y je přiřazen právě jeden bod v Kartézské soustavě souřadné a naopak.
Chceme-li popsat polohu bodu vzhledem k určité vztažné soustavě, musíme nejprve určit okamžik, v němž začneme měřit čas. Spojením soustavy souřadnic a měření času dostáváme vztažnou soustavu. Polohu hmotného bodu určujeme pomocí souřadnic. Nejčastěji používáme pravoúhlou - kartézskou soustavu souřadnic (název je odvozen podle francouzského matematika a filozofa René Descarta, latinsky Cartesia), jejímž základem jsou tři navzájem kolmé přímky x, y, z procházející společným bodem - počátkem souřadnic O (latinsky origo = počátek). Poloha hmotného bodu je určena souřadnicemi [x, y, z].
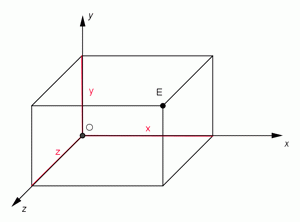
Určení polohy bodu pomocí souřadnic.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.
Často při popisu pohybu tělesa používáme jen dvě souřadnice, např. loď plující po moři, hod míčem apod. Třetí souřadnici považujeme za nulovou. Při pohybu tělesa se mění jeho souřadnice vzhledem ke zvolené souřadné soustavě v závislosti na čase. Geometrická čára, kterou těleso při pohybu opisuje, se nazývá trajektorie. Trajektorie se ale liší od tvaru grafu, který udává závislost dráhy na čase v pravoúhlých souřadnicích.
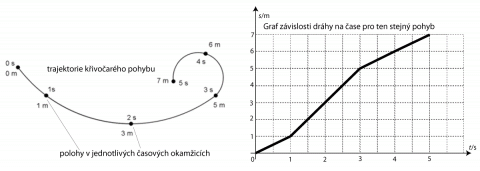
Souvislost mezi trajektorií a grafickým znázorněním závislosti dráhy na čase.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.
Pokud chceme vyznačit závislost dráhy na čase při nulové rychlosti (auto stojí) nebo při rychlosti na čase při konstantní rychlosti, pak grafem bude přímka rovnoběžná s osou x. Tato funkce se nazývá konstantní a je daná předpisem f(x) = c. Její obor hodnot obsahuje pouze jedno číslo (konstantu c). Definičním oborem této funkce je celá množina reálných čísel.
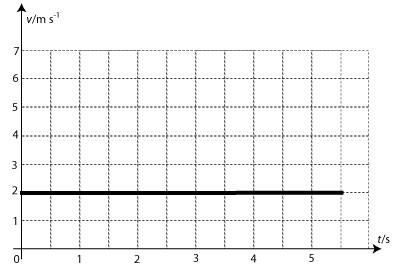
Graf konstantní funkce.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.
Pokud při pohybu je rychlost v daném úseku dráhy stejná, je grafem závislosti dráhy na čase přímka. Tato funkce se nazývá lineární a je daná rovnicí y = ax + b, kde a a b jsou reálná čísla, a je různé od nuly. Speciálním případem je přímá úměrnost, která je dána vztahem y = ax, kde b = 0, jejíž graf prochází počátkem soustavy souřadné.
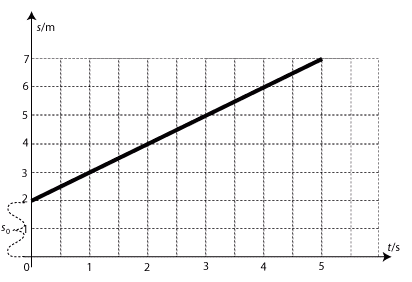
Závislost dráhy na čase u rovnoměrného pohybu.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.
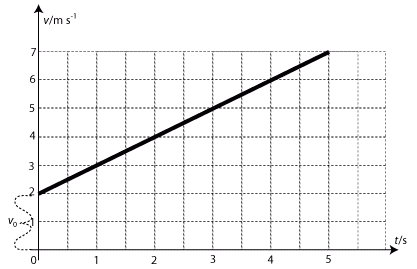
Grafická závislost rychlosti na čase u rovnoměrně zrychleného pohybu.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.
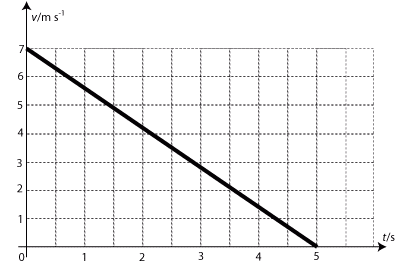
Grafická závislost rychlosti na čase u rovnoměrně zpomaleného pohybu.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.
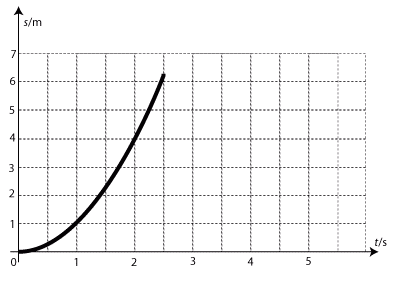
Pokud se rychlost při pohybu rovnoměrně zvětšuje nebo zmenšuje, pak je grafem část paraboly. Tato funkce se nazývá kvadratická a je dána ve tvaru y = ax2 + bx + c, kde a, b, c jsou reálná čísla a a je různé od nuly.