Teorie
Zlomky používali Egypťané už v 2. tisíciletí před n. l. Zapisovali tzv. kmenové zlomky (čitatel 1) pomocí hieroglyfů. Používali několik zvláštních zlomků, ostatní vyjadřovali pomocí kmenových zlomků, např.
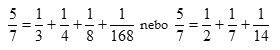
Již ve 2. století před naším letopočtem se v Číně používaly soustavy délkových jednotek, kde větší jednotka obsahovala 10 jednotek menších. Postupně se pak objevily i desítkové soustavy jednotek objemů a vah (hmotnosti) a z jednotek desetinné soustavy měr se vyvinuly desetinné zlomky. Tyto zlomky však zůstaly až do konce středověku těsně vázány na desetinné měření a víc se neuplatnily. V Evropě v souvislosti s rozvojem průmyslu a obchodu, mořeplavby, vědy a techniky vznikla potřeba velkých a obtížných aritmetických výpočtů, proto se úsilí matematiků té doby změřilo na objevování rozličných zjednodušených výpočtů, což nakonec vedlo k objevu desetinných čísel. Díky svým přednostem při výpočtech se stala desetinná čísla nedílnou součástí aritmetiky. Desetinnou čárku zavedl např. Johannes Kepler. Někteří matematikové, např. Christoph Clavius Schlüssel, zavedli desetinnou tečku.
Zlomek tedy představuje podíl dvou výrazů. Nad zlomkovou čárou je čitatel a pod zlomkovou čárou jmenovatel. Zlomek má smysl jen tehdy, pokud není ve jmenovateli nula (v oboru reálných čísel totiž nelze dělit nulou). V čitateli i jmenovateli se může nacházet další zlomek, pak se tento zlomek označuje jako složený. Pokud je ve zlomku jmenovatel větší než čitatel, označuje se tento zlomek jako pravý. Pokud je zlomek v kombinaci s celým číslem, např. 1 ½, pak se tento tvar označuje jako smíšený. Zlomky slouží k vyjádření částí celku, např. polovina ½, třetina 1/3 atd. Zlomek, ve kterém jsou oba výrazy celá čísla představuje zápis racionálního čísla. Tento zápis není jednoznačný, protože každé racionální číslo lze vyjádřit buď ve tvaru zlomku nebo v desetinném rozvoji ať už konečném nebo nekonečném periodickém. Mezi všemi těmito vyjádřeními existuje jediné, které má tu vlastnost, že čitatel a jmenovatel jsou nesoudělná (tj. jejich společným dělitelem je jenom číslo jedna). O takovém zlomku říkáme, že je vyjádřením daného racionálního čísla v základním tvaru. Nedá-li se číslo zapsat ve tvaru zlomku nebo je jeho desetinný rozvoj neperiodický, pak patří mezi iracionální čísla.
Racionální čísla v základním tvaru p/q a r/s porovnáváme na základě součinů p × s, q × r
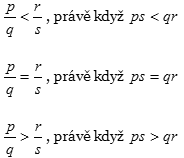
Pro početní operace s racionálními čísli p/q a r/s platí
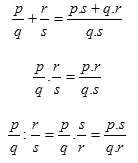
Zlomky můžeme přepsat jako procentuální podíl z celku. Stačí zlomek upravit tak, aby měl ve jmenovateli číslo 100. Hodnota čitatele pak představuje procenta. Příkladem může být třeba zlomek ¾ = 75/100 ─› 75 %.

