Teorie
První písemné záznamy o přirozených číslech pocházejí z Mezopotámie a Egypta z období asi 3500 před n. l. Jako přirozená čísla označujeme čísla, která používáme k vyjádření počtu prvků konečných neprázdných množin (počtu osob, zvířat, předmětů apod.) nebo pořadí prvků. Množinu přirozených čísel označujeme N a patří sem čísla 1, 2, 3, atd. Nula se objevila 2000 před n. l. v Babyloně, mezi lety 500 až 550 n. l. se objevila v pracích Arybhaty a odtud se dostala do evropské matematiky. Jako součást celých čísel se objevila nula až v roce 1200 v pracích Fibonacciho. Kromě přirozených čísel a nuly obsahují celá čísla i čísla záporná, která pochází z 5. století před n. l. z Řecka. Pravidla pro počítání se zápornými čísly doplnil Girolamo Cardano a Bombelli v 16. století. Množinu celých čísel označujeme Z a patří sem čísla …, -2, -1, 0, 1, 2, atd. Zlomky se objevily už 3000 před n. l. v Mezopotámii a Egyptě. Zlomky společně s celými čísly tvoří množinu racionálních čísel, kterou označujeme Q. Racionální čísla se používají k vyjádření počtu celků a jejich dílů, změn těchto počtů apod. Racionální čísla jsou čísla, která se dají zapsat ve tvaru zlomku, kde v čitateli i jmenovateli jsou celá čísla, ve jmenovateli nesmí být nula. Kladná iracionální čísla se objevila okolo roku 300 před n. l. ve spisech Eukleida. Množina iracionálních čísel se označuje I a patří sem √2, √5, π atd. Množina, která obsahuje všechna přirozená, celá, racionální a iracionální čísla se nazývá množina reálných čísel, značí se R.
Dělitelnost
O číslech 35 a 5 se můžeme vyjádřit tak, že číslo 35 je násobkem čísla 5 nebo že číslo 5 je dělitelem čísla 35. Obecně platí, že pro každé přirozené číslo existují dva dělitelé, tedy čísla, kterými se dá číslo dělit. Je to vždy číslo jedna a stejné číslo. Obě čísla se nazývají samozřejmí dělitelé. Abychom snadno našli dělitele daného čísla, můžeme použít následující znaky dělitelnosti.
|
2 |
číslo je sudé, tj. má poslední číslici 0, 2, 4, 6, 8 |
|
3 |
ciferný součet dělitelný třemi |
|
4 |
poslední dvojčíslí je dělitelné čtyřmi |
|
5 |
zápis čísla končí na 0 nebo 5 |
|
6 |
je dělitelné dvěma a zároveň třemi |
|
7 |
každou cifru čísla vynásobíme od konce číslem z řady 1,3,2,6,4,5 (řada se pak u dalších cifer opakuje) a vše sečteme a výsledný součet musí být dělitelný sedmi |
|
8 |
poslední trojčíslí je dělitelné osmi |
|
9 |
ciferný součet je dělitelný devíti |
|
10 |
zápis čísla končí nulou |
|
11 |
součet číslic lichých řádů je roven součtu číslic sudých řádů anebo se tyto součty liší o násobek jedenácti |
|
12 |
dělitelné třema a čtyřma |
|
13 |
číslo rozdělíme zprava na trojčíslí. Odečteme vždy ta na lichých místech od těch na sudých místech (lze i obráceně), výsledek je dělitelný 13 |
|
14 |
dělitelné dvěma a sedmi |
|
15 |
dělitelné třema a pěti |
Prvočísla
Prvočísla jsou všechna přirozená čísla, která mají právě dva různé dělitele, číslo jedna a samo sebe. Opakem jsou čísla složená, která mají aspoň tři různé dělitele. Číslo jedna nepovažujeme ani za prvočíslo, ani za složené číslo. Například číslo 40 není prvočíslo, protože je dělitelné 1, 2, 4, 5, 8, 10, 20 a 40. Ale číslo 41 je prvočíslo, protože je dělitelné 1 a 41.
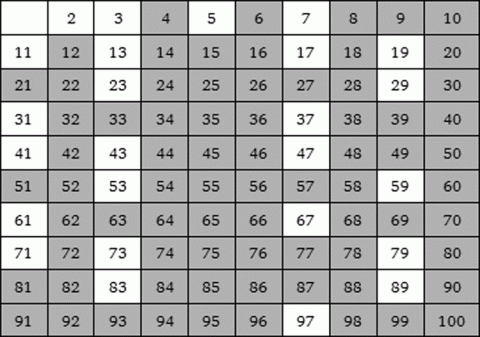
První čtyři prvočísla (2, 3, 5, 7) byla objevena už v dávnověku a další čtyři prvočísla (11, 13, 17, 19) se zachovala jako vruby na kosti z Ishanga. Kolik ale vlastně těch prvočísel je? Eratosthenes používal k vyhledávání prvočísel voskové tabulky s napsanými přirozenými čísly většími než jedna. Číslo dva ponechal a jehlou vypálil násobky dvou. Pak stejně postupoval s trojkou apod. Na konci výpočtu tabulka připomíná síto – tzv. Eratosthenovo síto.
Pokud chceme zjistit, zda je dané číslo prvočíslo, nemusíme zjišťovat, zda je dělitelné všemi prvočísli menšími. Stačí zjistit, zda je dělitelné pouze prvočísly menšími než jeho odmocnina. Zkoumáme např. číslo 211. Jeho odmocnina je asi 14,5. Stačí tedy zkontrolovat dělitelnost 211 čísly 2, 3, 5, 7, 11 a 13. Všechna tato dělení jsou se zbytkem, a proto číslo 211 je prvočíslem.
Euklides ve svých Základech dokázal, že prvočísel je nekonečně mnoho. Jednociferná jsou čtyři, dvojciferných je 21, trojciferných 143, čtyřciferných 1161, pěticiferných 8363 atd. Největší prvočíslo má 12,9 milionu číslic.
Pokud leží na číselné ose mezi dvěma prvočísly jen jedno další číslo, pak se obě prvočísla nazývají prvočíselná dvojčata. Příkladem může být třeba 3 a 5, 5 a 7, 11 a 13 atd. Už v starém Řecku se matematikové zabývali otázkou, zda takových prvočíselných dvojčat existuje nekonečně mnoho a jaká je jejich četnost. Díky počítačům sice generujeme další a další prvočíselná dvojčata, to však ale není důkaz. Stále však nebyl formulován přesný důkaz.
Pierre Fermat se domníval, že všechna čísla ve tvaru
jsou prvočísla. Prvních pět členů této posloupnosti 3, 5, 17, 257, a 65 537 prvočísla skutečně jsou. Avšak už v roce 1732 Leonhard Euler zjistil, že páté číslo 4 294 967 297 je složené, protože je dělitelné 641. Tato čísla se nazývají Fermatova čísla. V současné době je počet Fermatových prvočísel stále otevřeným problémem, předpokládá se, že kromě prvních pěti už žádná další prvočísla nejsou.Marin Marsenne sudoval čísla ve tvaru
kde p je prvočíslo. Jestliže je i Mp prvočíslo, nazývá se Marsennovo prvočíslo. Do dneška bylo nalezeno jen 47 Marsennových prvočísel. Těmito čísly se zabýval i Pierre Fermat a jeho výsledky ho dovedly k objevu Malé Fermatovy věty, která říká, že prvočíslo q dělí (beze zbytku) rozdíl 2q – 1 – 1.Vzorec na výpočet prvočísel přinesl i Leonhard Euler
. Platí pro každé přirozené číslo a až po číslo 39 opravdu dostaneme prvočísla. Mocniny a odmocniny
S pojmem mocnina se setkáváme už u starověkých Řeků při řešení geometrických úloh. Obsah čtverce, objem krychle a podobné problémy měření vedly k vytvoření pojmů druhé a třetí mocniny. Kroky vedoucí k vytvoření pojmů vyšších mocnin nebyly tak snadné. Nejprve bylo třeba odpoutat se od geometrické představy, která se spojovala s každým aritmetickým výkonem. Přesto se o čtvrté mocnině hovoří už u Herona z Alexandrie. Diofantos z Alexandrie uvádí možnost zápisu šesté mocniny, ale používá pouze třetí mocniny při řešení rovnic. Velký vliv na rozvoj pojmu mocniny a počítání s mocninami měly indické poznatky, které přinesl do Evropy Musa al-Chvárizmí a jiní. Trvalo však ještě velmi dlouho, než nauka o mocninách dosáhla své dnešní podoby. Nynější zápis mocnin zavedl ve svém díle Géométrie René Descartes.
Objev Pythagorovy věty pomohl prý pythagorejské škole zjistit, že úhlopříčka čtverce není vyjádřitelná racionálními hodnotami, tj. že její délku není možné vyjádřit jako celé nebo lomené číslo. Tento objev způsobil velký nesoulad v tehdejších řeckých filozofických a matematických poznatcích. Nemáme bezpečnou zprávu o tom, jak Archimédes určoval druhé odmocniny ve svých výpočtech. Používal pravděpodobně, stejně jako Heron, přibližnou hodnotu podle vzorce
Tento způsob odmocňování znali prý už Babyloňané. Znak odmocniny se objevil na konci 15. století. Současný znak se začal používat už Simon Stevin a Albert Girard na konci 16. století a poupátkem 17. století.
N-tou mocninu definujeme pro každé reálné číslo a a každé celé číslo n jako an = a · a · a ·…· a, kde a se násobí celkem n-krát. Číslo a se nazývá základ mocniny nebo mocněnec, číslo n exponent nebo mocnitel. Pro každé reálné číslo a různé od nuly je a0 = 1.
Podobně můžeme pro libovolné přirozené číslo n definovat n-tou odmocninu z nezáporného čísla a jako takové nezáporné číslo b, pro něž platí bn = a, označujeme
Číslo a se nazývá základ odmocniny nebo odmocněnec, číslo n odmocnitel. Odmocnina je vlastně mocnina s racionálním mocnitelem
