Lodě se mohou potopit z různých důvodů. Záhadně mizí lodě a letadla v bermudském trojúhelníku. Ten tvoří Bermudské ostrovy společně s oblastí Miami na Floridě a Portorikem. Bermudský trojúhelník není oficiální zeměpisný název, jedná se o téměř rovnostranný trojúhelník s ramenem cca 1 600 km dlouhým. Bermudské ostrovy jsou zámořským územím Spojeného království. Leží v Atlantském oceánu u jihovýchodního pobřeží Spojených států ve střední části Severoamerické pánve.
 Bermudský trojúhelník.
Bermudský trojúhelník.
Zdroj: commons.wikimedia.org. Public domain.
Teorie
Z vlastní zkušenosti víme, že tělesa ponořená ve vodě se zdají být lehčí než na vzduchu. Ve vodě totiž na těleso působí síla, kterou nazýváme vztlaková síla Fvz a má opačný směr než tíhová síla FG.
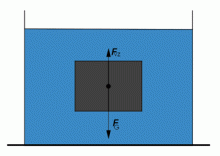
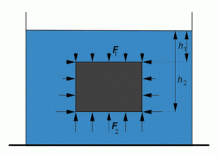 Působení sil na těleso ponořené v kapalině.
Působení sil na těleso ponořené v kapalině.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.
Vztlaková síla vzniká jako výslednice hydrostatických sil působících na povrchu tělesa v kapalině v klidu. Uvažujme těleso tvaru kvádru s podstavou o plošném obsahu S a výšce h, které je zcela ponořeno v kapalině o hustotě ρ. Podstavy kvádru jsou rovnoběžné s vodorovným povrchem kapaliny. Na všechny stěny kvádru působí kapalina hydrostatickými tlakovými silami. Tlakové síly působící na boční stěny jsou stejně velké a opačného směru, proto se vzájemně ruší. Na horní podstavu v hloubce h1 působí tlaková síla F1 o velikosti F1 = ρSh1g, na dolní podstavu v hloubce h2 tlaková síla F2 o velikosti F2 = ρSh2g. Výslednice sil F1 a F2 je vztlaková síla Fvz o velikosti
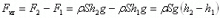
vzhledem k tomu, že h = h2 – h1
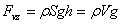
kde V = Sh je objem kvádru.
Poněvadž ve vztahu Fvz = ρVg představuje součin ρV hmotnost m kapaliny stejného objemu, jako je objem ponořeného tělesa, a součin ρVg = mg tíhu kapaliny o tomto objemu, můžeme říci, že velikost vztlakové síly Fvz se rovná tíze kapaliny o objemu ponořené části tělesa.
 Archimedes.
Archimedes.
Zdroj: Techmania Science Center. Autor: Pavel Trnka. Under Creative Commons.
K tomuto poznatku dospěl již ve 3. století př. n. l. Archimédes. Podle Vitruvia se o něm vypráví, že dostal za úkol od krále Hierona zjistit, zda zlatníci vyrobili celou korunu z přesně odváženého zlata. Jednou, když se koupal, tak si všiml, že z vany odtéká přesně stejné množství vody, jako je objem ponořené části těla. S výkřikem „HEUREKA, HEUREKA!!!“ (objevil jsem) pádil prý tehdy nahý ulicemi Syrakus, sledovaný udivenými spoluobčany. Jeho poznatky o vztlakové síle dnes shrnujeme pod názvem Archimédův zákon:
Těleso ponořené do kapaliny je nadlehčováno vztlakovou sílou, jejíž velikost se rovná tíze kapaliny stejného objemu, jako je objem ponořeného tělesa.
Podobně jako v kapalinách jsou tělesa nadlehčována také v plynech. Vzhledem k velmi malé hustotě plynů je vztlaková síla působící na těleso umístěné v plynu mnohem menší než vztlaková síla působící na totéž těleso v kapalině.
Důsledkem Archimédova zákona je různé chování těles v kapalině. Na těleso působí vztlaková síla Fvz a tíhová síla Fg. Výslednice působících sil má směr síly větší a velikost rovnou rozdílu velikostí obou sil. Porovnáváme–li velikosti těchto sil, může nastat jeden ze tří případů:
FG < Fvz, ρT < ρ – těleso plove na hladině
FG > Fvz, ρT > ρ – těleso klesá ke dnu
FG = Fvz, ρT = ρ – těleso se vznáší v kapalině.
Tyto případy platí i pro ohraničený objem plynu anebo kapaliny. Olej plave na vodě, voda plave na rtuti.
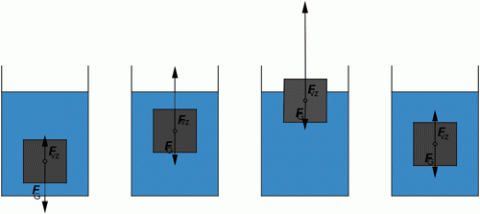 Různé možnosti poměru vztlakové a tíhové síly.
Různé možnosti poměru vztlakové a tíhové síly.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.
Zajímavost z fyziky:
Kromě velké frekvence lodní a letecké dopravy, která s sebou nese i větší výskyt havárií a ztroskotání, je vysvětlení záhady bermudského trojúhelníku jednoduché. Částečně lze záhadu vysvětlit pomocí přítomnosti velkého množství hydrátu methanu, který je vzhledem k hloubce kolem 6 000 m díky vysokému tlaku vody v pevném stavu. Čas od času se ale oddělí část této stlačené látky a zvolna stoupá k hladině. Jak klesá tlak okolní vody, začíná se hydratovaný methan přeměňovat na plyn, takže při dosažení mořské hladiny vznikne obří bublina o průměru i několika set metrů. Pro proplouvající loď nebo letadlo letící v nízké výšce se může stát osudnou. Sníží se totiž hustota vody nebo vzduchu a loď i letadlo klesnou ke dnu. Další hrozbou je možná exploze metanu nebo jeho jedovatost pro posádku.