Věda a technika v pozadí
Tanec
Teorie
Pokud nějaký předpis zobrazuje jeden bod na druhý, tak se nazývá zobrazení v rovině. Pokud se celý útvar zobrazí na ten stejný, tak se zobrazení nazývá shodné. Mezi shodná zobrazení patří osová souměrnost, středová souměrnost, posunutí a otočení. Mnohé předměty jsou soměrné podle osy, tzn. že je lze rozdělit na dvě stejné půlky. Třeba lidský obličej. Řada útvarů je souměrných podle více os. Např. čtverec má čtyři nebo kruh nekonečné mnoho os souměrnosti.
Osová souměrnost je dána přímkou o, která se nazývá osa souměrnosti. Osová souměrnost s osou o pak přiřazuje každému bodu, který neleží na ose o bod tak, že spojnice obou bodů je kolmá na osu o a ta je zároveň osou úsečky tvořené oběma body. O obou bodech se říká, že jsou souměrně sdružené podle osy souměrnosti. Pokud leží bod na ose, pak se v osové souměrnosti zobrazuje sám na sebe, a říkáme, že osa o je samodružná. Osová souměrnost je nepřímá shodnost.

Zobrazení v osové souměrnosti.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.
Středová souměrnost je dána bodem S, středem souměrnosti. Středová souměrnost se středem S přiřazuje každému bodu bod tak, že střed S je zároveň středem úsečky tvořené oběma body. O obou bodech se říká, že jsou souměrně sdružené podle středu souměrnosti. Bod S je samodružný, je mu tedy přiřazen ten stejný bod. Středová souměrnosti je přímá shodnost.
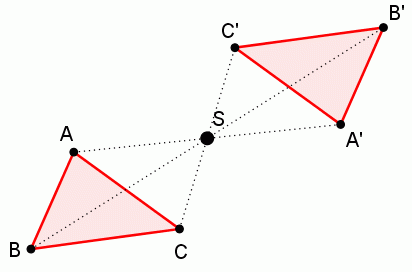
Zobrazení ve středové souměrnosti.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.
Slovo symetrie pochází z řekých slov sym a metrie, které znamenají stejné měřítko. Už Platon a Aristeles spojili pojem symetrie s krásou. Symetrie totiž hraje v přírodě velkou roli. Symetrické je lidské tělo, většina živočichů, rostlin, květů, krystaly, vločky, kapky, ovocné plody atd. Matematickým jazykem, který popisuje podstatu symetrií a zkoumá jejich vlastnosti, je teorie grup. Jednou ze základních a nejčastějších symetrií v přírodě je symetrie vůči změně měřítka - tzv. škálovací symetrie. S touto symetrií souvisí tzv. fraktální geometrie a pojem fraktálu.
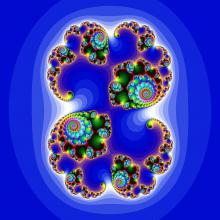
Fraktál.
Zdroj: commons.wikimedia.org. Public domain.

