Čtvercovými čísly se zabývali pythagorejci a jsou to čísla, která představují počet třeba teček ve čtverci.
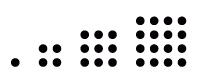
Znázornění čtvercový čísel.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.
První čtvercové číslo je 1. Pro pythagorejce nejdůležitější číslo spjaté s duchovní existencí. Pak pokračují čísla 4, 9, 16, 25, 36, 49, 64, …, která se nazývají dokonalé čtverce. Čtvercové číslo vypočítáme tak, že k předešlému čtverci připočítáme tečky, které přiléhají k předchozímu tvaru, například 9 + 7 = 16.
Pythagoras ale nezůstal pouze u čtverců. Zabýval se také dalšími útvary, jako jsou trojúhelníky, pětiúhelníky a další mnohoúhelníky. Mezi trojúhelníková čísla patří 1, 3, 6, 10, 15, 21, 28, 36, … Trojúhelníkové číslo vypočítáme tak, že k předchozímu číslu přičteme počet teček v dalším řádku. Další možná definice trojúhelníkového čísla je, že je to takové číslo, které můžeme rozložit na součet čísel 1, 2, 3, … . První trojúhelníkové číslo je 1, další je 3 (= 1 + 2), další je 6 (= 1 + 2 + 3) atd. Všechna celá čísla mají zajímavou vlastnost: Každé celé číslo se dá rozložit jako součet maximálně tří trojúhelníkových čísel! (např. 32 = 28 + 3 + 1)

Znázornění trojúhelníkových čísel.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.
Když porovnáme čtvercová a troúhelníková čísla, tak zjistíme, že v obou se nachází číslo 36. Pokud sečteme dvě po sobě jdoucí trojúhelníková čísla, získáme čtvercové číslo. Důkazem této věty je třeba tento obrázek, který lze zobecnit.

Důkaz, že součet dvou po sobě jdoucích trojúhelníkových čísel je číslo čtvercové.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.
Obecně tedy můžeme sestrojit čísla mnohoúhelníková. Ta tvoří aritmetickou posloupnost přirozených čísel ve tvaru 1, 1 + d, 1 + 2d, 1 + 3d. Pro d = 1 dostaneme trojúhelníková čísla, pro d = 2 čtvercová, pro d = 3 pětiúhelníková čísla atd. Mezi šestiúhelníková čísla patří 1, 7, 19, 37.
Podobným způsobem je možné zkonstruovat i čísla v prostoru. Pak se nazývají pyramidová. Mohou mít v podstatě jakýkoli mnohoúhelník v podstavě. Vzniknou tak třeba čtvercová pyramidová čísla: 1, 5, 14, 30, …
Použité zdroje:
[1] CRILLY, T. Matematika. 50 myšlenek, které musíte znát. 1. vydání. Praha: Slovart, 2010. ISBN: 978-80-7391-409-7.
[2] TRENČANSKÝ, I. O pyramidálních číslach. Rozhledy matematicko–fyzikální, roč. 82 (2007), č. 3, s. 1-6. ISSN 0035-9343.
[3] SEIBERT, J. Pythagorejské trojice trojúhelníkových čísel. Matematika Fyzika Informatika: časopis pro výuku na základních a středních školách, 2004/2005, roč.14, s. 385-393. ISSN 1210-1761.
[4] SPENCER, A. Kniha čísel. 1. vydání. Praha: Albatros, 2005. ISBN: 13-805-KMČ-005.
