Vyjadřovat množství věcí pomocí přirozených čísel dovedli zřejmě lidé v mladší době kamenné (asi před 10 000 lety). První písemné záznamy o přirozených číslech pocházejí z Mezopotámie a Egypta z období asi 3500 před n. l. Jako přirozená čísla označujeme čísla, která používáme k vyjádření počtu prvků konečných neprázdných množin (počtu osob, zvířat, předmětů apod.) nebo pořadí prvků. Množinu přirozených čísel označujeme N a patří sem čísla 1, 2, 3 atd. Krátce po zavedení přirozených čísel, začal člověk používat operace sčítání, odčítání, násobení a dělení. Otázkou je, zda si s přirozenými čísly vystačíme při provádění těchto operací. Pokud sečteme nebo vynásobíme přirozená čísla, výsledek bude zase číslo přirozené. Pokud budeme chtít odečítat, tak zjistíme, že odčítat přirozená čísla lze jen tehdy, když odčítáme menší číslo od většího. Pokud budou obě čísla stejná, výsledek bude nula. Musíme tedy k přirozeným číslům přidat číslo nové – nulu.

Znázornění některých přirozených čísel na číselné ose.
Zdroj: Techmania Science Center. Autor. Magda Králová.
Poprvé nalezneme nulu v zápisech babylonských matematiků a astronomů zhruba 2000 let před n. l. Měla podobu dvou šikmých klínových znaků a nepředstavovala ještě skutečnou číslici, pouze označení prázdného prostoru na místě jednotek, desítek nebo stovek. Nezávisle na Babyloňanech zřejmě objevili nulu i Mayové. V klasické epoše mayských dějin tu kněží vytvořili číselný systém začínající právě nulou. Znázorňovali ji buď jako pitoreskní obličej nebo v podobě mušle či ulity. Ani u Mayů však nefungovala jako skutečné číslo a vyznačovala pouze prázdné místo příslušného řádu. Početní úkony s využitím nuly jako plnohodnotného čísla jsou doloženy poprvé u Indů. Nulu jako číslo používal Brahmagupta, který stanovil pravidla pro počítání s nulou. Jestliže nulu přičteme nebo odečteme, číslo se nezmění, při vynásobení nulou však náhle vše zmizí a dostaneme pouhou nulu. Do Evropy přinesl nulu Leonardo Pisánský (Fibonacci) v díle Liber Abaci (Kniha o abaku) z roku 1202. Fibonacci píše: „devět indických obrazců jsou 9 8 7 6 5 4 3 2 1. Pomocí těchto obrazců a znaku 0, který Arabové nazývají zephirum, lze zapsat jakékoliv číslo“. Používání nuly v matematických úkonech se brzy stalo pro italské kupce a bankéře nezbytností a Itálie se stala vzorem pro celý finanční svět. Navzdory prokázané užitečnosti zůstávala však nula v křesťanském světě ještě dlouho něčím záhadným či dokonce podezřelým.
Vraťme se k odčítání přirozených čísel. Pokud se odčítá větší číslo od menšího, nedá se výsledek pomocí přirozeného čísla vyjádřit. Takovému výsledku se začalo říkat dluh už v Číně v prvním tisíciletí před n. l. S tímto pojmem si vystačila matematika až do 18. století. Tehdy Leonhard Euler, Isaac Newton nebo René Descartes začali zavádět záporná čísla. Souhrný název pro přirozená čísla, nulu a záporná čísla je čísla celá. Pravidla pro počítání se zápornými čísly doplnil Girolamo Cardano a Rafael Bombelli v 16. století. Množinu celých čísel označujeme Z a patří sem čísla …, -2, -1, 0, 1, 2, atd.
Znázornění některých celých čísel na číselné ose.
Zdroj: Techmania Science Center. Autor. Magda Králová.
Zbývá poslední základní operace – dělení přirozených čísel. U některých se nám to podaří a výsledek je přirozené číslo, např. 6 děleno 3 je 2. Ale u některých dělit nelze, např. 6 děleno 4. Výsledek nemůžeme vyjádřit jako přirozené číslo. Byla proto zavedena nová čísla – zlomky, které se poprvé objevily už 3000 před n. l. v Mezopotámii a Egyptě. Zlomky společně s celými čísly tvoří množinu racionálních čísel (z latinského ratio – rozum), kterou označujeme Q. Racionální čísla se používají k vyjádření počtu celků a jejich dílů, změn těchto počtů apod.
To jsou čtyři základní operace, které lze provádět v oboru racionálních čísel. V matematice je ale řada dalších operací, např. odmocňování. Odmocnit některá racionální čísla není problém, např. odmocnina ze 4 je plus nebo mínus dvě. Co ale když budeme chtít odmocnit 2? V rozvoji se žádná skupina číslic neopakuje, nejedná se tedy o číslo racionální s periodickým rozvojem, ale o nový druh čísel, které se nazývají iracionální. Kladná iracionální čísla se objevila okolo roku 300 před n. l. ve spisech Eukleida. Množina iracionálních čísel se označuje I a patří sem √2, √5, π atd. Množina, která obsahuje všechna přirozená, celá, racionální a iracionální čísla se nazývá množina reálných čísel, značí se R.
Pokud chceme zapsat jen část některé množiny čísel, pak u přirozených a celých čísel použijeme zápis pomocí množin, např. {5, 6, 7}. U reálných čísel musíme použít zápis pomocí intervalů, které používají jako ohraničení dva typy závorek: ( znamená, že krajní bod do intervalu nepatří, < znamená, že krajní bod do intervalu patří. Zápis intervalu <1;5) pak znamená, že je dána část číselné osy mezi 1 a 5, ale do intervalu patří pouze krajní bod 1.

Znázornění intervalu <1;5). Zdroj: Techmania Science Center. Autor. Magda Králová.
Odmocňování se nám může objevit i při řešení třeba této kvadratické rovnice x2 + 1 = 0, jejíž řešení vede na x2 = -1. Aby rovnice měla řešení, byla zavedena komplexní jednota i, pro kterou platí i ∙ i = i2 = -1. Komplexní jednotka je součástí imaginárního čísla (třeba 4i), jehož označení pochází od René Descartesa, který tak označil kuriózní řešení rovnic. Komplexní číslo se zapisuje jako dvojčlen a1 + a2i, kde a1, a2 jsou reálná čísla. V zápisu a1 + a2i komplexního čísla se číslo a1 nazývá jeho reálná část, a2 jeho imaginární část. Množina komplexních čísel se značí C.
Poprvé byla komplexní čísla zavedena v teorii kubických rovnic (rovnic třetího stupně). Jejich řešením se zabýval Girolamo Cardano, který dospěl ke vztahům, které vyjadřovaly kořeny rovnic jako součet nebo rozdíl čísel komplexních. Cardanův současník, Rafael Bombelli, vypracoval teorii ryze imaginárních čísel a řešil kvadratické rovnice, které mají komplexní kořeny. Komplexními čísly se později zabýval Gottfried Leibniz, Abraham de Moivre a Leonhard Euler. Moivre i Euler zdůraznili význam a použití komplexních čísel v různých matematických oborech; Euler zavedl označení pro imaginární jednotku. V roce 1799 Caspar Wessel zjistil, že lze komplexní čísla znázornit v tzv. komplexní rovině (nebo Gaussově rovině). Obrazem komplexního čísla a1 + a2i je bod, jehož první souřadnice v pravoúhlé soustavě souřadnic v rovině je a1, druhá a2, tj. bod A = [a1; a2]. Při tomto znázornění se reálná čísla zobrazí na osu x, ryze imaginární čísla na osu y. Proto se x-ová osa nazývá osa reálná, y-ová osa imaginární.
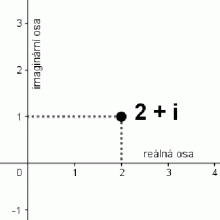
Znázornění komplexního čísla v Gaussově rovině.
Zdroj: Techmania Science Center. Autor. Magda Králová.
Komplexní čísla se používala velmi často. Přispěly k tomu i práce o komplexních číslech Karla Gausse a Williama Hamiltona. V novější době jsou komplexní čísla, a zejména pak teorie funkcí komplexní proměnné (tj. funkcí, jejichž definičním oborem je množina komplexních čísel), důležitým prostředkem při řešení mnoha technických problémů. Používají se např. při studiu aerodynamiky a elektrotechniky.
Matematici hledali zobecnění komplexních čísel. Komplexní čísla jsou dvourozměrná, proto se William Hamilton pokusil najít čísla trojrozměrná. Bez úspěchu. Podařilo se mu to až s čísly čtyřrozměrnými, která se dnes označují jako kvaterniony. Kvaterniony se vyjadřují podobně jako komplexní čísla ve tvaru a + bi + cj + dk, platí i2 = -1, j2 = -1, k2 = -1. Zajímavostí je, že záleží na pořadí čísel při násobení (i × j = k, j × i = -k). Kvatenriony našly využití v navigaci, robotice i v počítačích. Krátce nato objevil Arthur Cayley čísla s osmi rozměry, která se nazývají oktoniony nebo-li Cayleyho čísla. Počítání s oktoniony je ještě divočejší a překvapující. Pokračování s dalšími rozměry se tentokrát nekonalo. 50 let po Hamiltonově objevu bylo dokázáno, že další n-rozměrná čísla neexistují (pro n ≠ 2, 4, 8).
Použité zdroje:
[1] BEUTELSPACHER, A. Matematika do vesty. Praha: Baronet, 2005. ISBN 80-7214-841-9.
[2] CRILLY, T. Matematika. 50 myšlenek, které musíte znát. 1. vydání. Praha: Slovart, 2010. ISBN: 978-80-7391-409-7.
[3] CRILLY, T. Velké otázky. Matematika. Praha: Knižní klub, 2012. 1. vydání. ISBN: 978-80-242-3596-7.
[4] PETRÁNEK, O. – kol. Matematika pro střední odborné učiliště a studijní obory středních odborných učilišť 4. část. Praha: Státní pedagogické nakladatelství, 1986. ISBN 14-227-86.
[5] URBANOVÁ, J. Matematika pro 5. ročník II. díl. Praha: Státní pedagogické nakladatelství, 1989. ISBN 14-578-89.
