Protože nemůžeme zjistit skutečnou rychlost každé jednotlivé molekuly plynu, musíme pracovat jen se statistickými údaji o rychlostech molekul plynu. Anglický fyzik James Maxwell definoval funkční závislost, která vyjadřuje rozdělení rychlostí molekul v ideálním plynu.
James Clerk Maxwell.
Zdroj: Techmania Science Center. Autor: Pavel Trnka. Under Creative Commons.
Vzájemné srážky molekul a srážky molekul se stěnami nádoby způsobují, že se jejich rychlost neustále mění co do velikosti i co do směru. Proto se v každém okamžiku mění i kinetická energie posuvného pohybu těchto částic. Srážky molekul ideálního plynu jsou ale pružné, proto za stálé teploty je celková kinetická energie plynu konstantní. To ale znamená, že na každou molekulu připadá stejná střední kinetická energie
kde N je počet molekul. Tento poznatek můžeme vyslovit také tak, že každé molekule hmotnosti m0 můžeme přiřadit takovou rychlost vk odpovídající kinetické energii
Rychlost vk se nazývá střední kvadratická rychlost. Je to taková rychlost, jakou by se musely pohybovat všechny molekuly, aby se celková kinetická energie posuvného pohybu molekul nezměnila. Je jasné, že rychlosti molekul ve velkém souboru, nejsou stejné. Dá se předpokládat, že malé množství molekul se pohybuje velmi rychle nebo velmi pomalu a velká část částic se pohybuje rychlostí blízkou střední kvadratické rychlosti. Maxwell použil statistické metody a teoreticky dokázal, že střední kvadratická rychlost je závislá na termodynamické teplotě plynu T a na hmotnosti m0 molekuly plynu podle vztahu
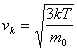
kde k = 1,38 ∙ 10-23 J K-1 je Boltzmannova konstanta, kterou poprvé určil v roce 1900 Max Planck, když ji potřeboval pro formulaci svého vyzařovacího zákona. V roce 1972 byla uveřejněna nová, přesnější metoda založená na měření rychlosti zvuku v akustickém interferometru, při níž se využívá závislosti rychlosti zvuku na tlaku a hustotě.
Střední kvadratické rychlosti molekul některých plynů pro různé teploty jsou uvedeny v MFChT. Např. při teplotě 273,15 K mají molekuly plynů vzduchu rychlost vk = 485 m s-1. Nahodilými srážkami mohou molekuly plynů vzduchu získat i rychlost větší, než je úniková rychlost v zemském gravitačním poli (11,2 km s-1 při povrchu Země), a uniknout tak ze zemské atmosféry. Počet těchto molekul je však ve srovnání s celkovým počtem molekul v atmosféře tak malý, že Země prakticky atmosféru neztrácí. Na povrchu Měsíce je úniková rychlost mnohem menší (2,4 km s-1), a proto Měsíc nemůže mít atmosféru.
Vztah pro střední kvadratickou rychlost molekul můžeme použít k výpočtu střední kinetické energie, kterou má jedna molekula ideálního plynu v důsledku svého neuspořádaného posuvného pohybu
Molekuly ideálního plynu mají v důsledku neuspořádaného posuvného pohybu střední kinetickou energii, která je přímo úměrná termodynamické teplotě plynu. Z tohoto vztahu také vyplývá, že je–li teplota dvou různých ideálních plynů stejná, pak molekuly těchto plynů mají stejnou střední kinetickou energii. To však znamená, že molekuly o menší hmotnosti se pohybují větší rychlostí než molekuly o větší hmotnosti.
