Objem plynu nebo jiné pracovní látky se nemůže neustále zvyšovat, protože rozměry pracovního válce jsou konečné. Proto práce, kterou může vykonat plyn uzavřený ve válci s pístem, má omezenou velikost. Chceme–li, aby tepelný stroj pracoval trvale, musíme zabezpečit, aby se plyn po ukončení expanze vrátil do původního stavu. Děj, při kterém počáteční stav soustavy je totožný s konečným stavem, se nazývá kruhový děj. V pracovním diagramu je kruhový děj znázorněn uzavřenou křivkou (viz obrázek). Obsah plochy uzavřené křivkou znázorňuje celkovou práci vykonanou pracovní látkou během jednoho kruhového děje. Tento kruhový děj (cyklus) se může mnohokrát opakovat, takže tepelný stroj uskutečňující kruhový děj může trvale vykonávat práci.
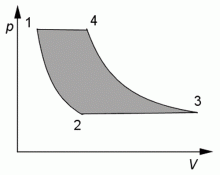
Grafické znázornění práci při kruhovém ději.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.
Při ukončení jednoho kruhového děje je celková změna vnitřní energie pracovní látky nulová. Těleso, od kterého pracovní látka přijme během jednoho kruhového děje teplo Q1, se nazývá ohřívač. Těleso, kterému předá teplo Q2, se nazývá chladič. Celkové teplo, které pracovní látka přijme během jednoho kruhového děje, je Q = Q1 – Q2. Celková práce, kterou vykoná pracovní látka během jednoho kruhového děje, se rovná celkovému teplu přijatému během tohoto děje od okolí. Kolem poloviny 18. století se Sadi Carnotovi, Emile Clapeyronovi, Jamesi Jouleovi a Williamu Thomsonovi podařilo zjistit, kolik tepla z ohřívače se dá v nejlepším případě přeměnit v užitečnou práci a kolik zůstane znehodnoceno. Nalezli jednoduchý vztah
S využitím tohoto vztahu můžeme napsat pro celkovou práci
![]()
Aby získané práce bylo skutečně tolik, museli bychom zamezit veškerému tření, veškerým kontaktům těles o různých teplotách, které by způsobily tok tepla bez užitku atd. Pokud se nám to nepodaří, bude získaná práce vždy menší. Maximální účinnost h libovolného kruhového děje vyjádříme vztahem, který dokázal Sadi Carnot
![]()
Tento vztah určuje horní hranici účinnosti tepelných strojů. Podle tohoto vztahu je účinnost tepelného stroje tím vyšší, čím vyšší je teplota ohřívače (např. teplota páry u parních strojů) a čím nižší je teplota chladiče (např. teplota vycházející páry z parního stroje). Skutečná účinnost kruhového děje je vždy podstatně menší než horní hranice účinnosti, neboť vznikají nejrůznější tepelné ztráty. Např. parní turbína pracuje mezi teplotami asi 800 K a 320 K, takže maximální účinnost je kolem 60 %, skutečná však mezi 25 a 35 %.
Za předpokladu, že chceme mít stroj o maximálním výkonu, použijeme upravený Carnotův vztah, který v roce 1957 odvodil Igor Novikov. Do podvědomí se dostal pod názvem Curzonův – Ahlbornův vztah
![]()
V následující tabulce je porovnání Carnotovy tepelné účinnosti, Curzonovy – Ahlbornovy účinnosti a skutečné účinnosti pro některé elektrárny a motory
|
Elektrárna |
T2 (°C) |
T1 (°C) |
Carnotova tepelná účinnost |
Curzonova – Ahlbornova účinnost |
skutečná účinnost |
|---|---|---|---|---|---|
|
West, Thurrock |
25 |
565 |
64,1 % |
40 % |
36 % |
|
CANDU |
25 |
300 |
48 % |
28 % |
30 % |
|
Larderello |
80 |
250 |
32,3 % |
17,5 % |
16 % |
|
parní turbína |
320 |
800 |
60 % |
31 % |
30 % |
Carnotův ideální stroj pracuje v cyklu čtyř po sobě jdoucích vratných dějů, z nichž první a třetí jsou izotermické a druhý a čtvrtý jsou adiabatické. Existuje i Stirlingův motor, který pracuje v cyklu izotermické komprese, izochorického děje, izotermické expanze a celý cyklus je uzavřen izochorickým dějem. Stirlingův motor pracuje hospodárně, ekologicky a nehlučně. Nevýhodou je potřeba velké chladící plochy a pomalého rozběhu. Používá se k pohonu elektrogenerátorů, zkapalňovačů plynů apod.
