Teorie
Kdy působí gravitační síla, kdy tíhová a kdy tíha? Z této šlamastiky se dostaneme jednoduše. Každá dvě tělesa se přitahují gravitační silou Fg, která způsobuje gravitační zrychlení ag. Dosazením Newtonova gravitačního zákona do druhého Newtonova zákona získáme pro gravitační zrychlení vztah
![]()
kde M je hmotnost planety, r je jeho poloměr a koeficient κ [kapa] = 6,67 · 10-11 N m2 kg2 se nazývá gravitační konstanta. Gravitační zrychlení nezávisí na hmotnosti padajícího tělesa, jeho hodnota závisí pouze na hmotnosti planety, poloměru a gravitační konstantě. V tabulce jsou uvedeny hodnoty gravitačního zrychlení na různých planetách.
| Planeta | Gravitační zrychlení (m/s2) |
|---|---|
| Měsíc | 1,62 |
| Mars | 3,69 |
| Merkur | 3,70 |
| Uran | 8,69 |
| Venuše | 8,87 |
| Saturn | 8,96 |
| Země | 9,79 |
| Neptun | 11,15 |
| Jupiter | 23,12 |
Jenže situace není tak jednoduchá, protože se planety otáčí kolem své osy a do hry se dostává i odstředivá síla směřující od osy otáčení.
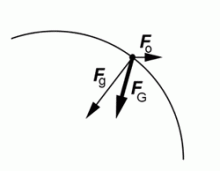
Na všechna tělesa na povrchu planety působí tedy dvě síly: gravitační síla Fg, směřující ke středu Země a odstředivá síla Fo, směřující od osy otáčení Země. Výslednicí obou sil je tíhová síla FG, která se vypočítá jako
![]()
Kde g je tíhové zrychlení.
Tíhová síla nesměřuje přesně do středu planety. Způsobuje zploštění Země. Nejvíce viditelný je tento jev u planety Saturn, který se otáčí velmi rychle a rozdíl mezi rovníkovým a polárním průměrem je 13 100 km.

Saturn.
Zdroj: www.nasa.gov.
Velikost gravitační síly Fg je pro dané těleso na všech místech zemského povrchu stejná, velikost odstředivé síly Fo se však mění se zeměpisnou šířkou. Na zemských pólech je nulová, proto je tíhová síla rovna gravitační síle. Vzdalujeme–li se od pólů, zvětšuje se poloměr r kruhové trajektorie příslušného místa na povrchu Země a odstředivá síla se zvětšuje. Tíhová síla FG má pak menší velikost než gravitační síla Fg a má také jiný směr – nesměřuje do středu Země. Největší velikost má odstředivá síla na zemském rovníku. Tíhová síla FG má proto na rovníku nejmenší velikost, směřuje ke středu Země. Na rovníku je asi 9,78 m s–2, na pólech asi 9,83 m s–2, u nás přibližně 9,81 m s–2 a pro praktické výpočty používáme hodnotu 10 m s–2.
Tíhové zrychlení závisí i na blízké hmotě, např. na Etně je g o 0,00292 m s–2 větší než normální hodnota nebo na nadmořské výšce – s rostoucí nadmořskou výškou se zmenšuje
![]()
Jeho změny však nejsou pro tělesa na povrchu Země příliš velké, proto můžeme velmi často považovat pro řešení dané úlohy tíhové zrychlení za konstantní, pokud jde o směr i velikost.
Působení tíhové síly na těleso nemá vždy pohybové účinky. Jestliže těleso leží na stole nebo je pověšeno, tak působí těleso tlakovou silou na stůl nebo tahovou silou na závěs. Tuto sílu pak nazýváme tíha tělesa G. Existence tíhové síly umožňuje vážení. A kolik bychom tedy navážili na pružinových vahách na jednotlivých planetách? Při použití kilogramového závaží udává hodnoty tabulka.
| Planeta | Tíha jednoho kilogramu |
|---|---|
| Měsíc | 0,17 |
| Mars | 0,38 |
| Merkur | 0,38 |
| Uran | 0,89 |
| Venuše | 0,90 |
| Saturn | 0,92 |
| Země | 1,00 |
| Neptun | 1,14 |
| Jupiter | 2,36 |