Při odvození Newtonova zákona můžeme kopírovat postup Isaaca Newtona tak, jak ho popsal ve svých Principiích. K tomu je ale nutná znalost diferenciálního počtu. Proto přeskočíme o několik století dál a použijeme důkaz Richarda Feynmana, ke kterému stačí středoškolská matematika. Tento důkaz nebyl zařazený do slavných Feynmanových přenášek, i když po přednášce 13. března 1964 zaujal řadu lidí. Jeho rukopisné poznámky se záhy ztratily a byly znovu nalezeny až v roce 1992 v pracovně jeho bývalého spolupracovníka Leightona.
Na trajektorii planety si zvolíme tři body A, B, C, ve kterých se planeta bude nacházet vždy za stejný časový interval. Do obrázku vyznačíme úsečky spojující dané body a Slunce, které jsou obecně různě dlouhé; úhly α, β, které jsou díky měnící se obvodové rychlosti také různé a vektory obvodové rychlosti u, v.

K odvození Newtonova gravitačního zákona.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.
Pokud by se planeta pohybovala podle zákona setrvačnosti, pak by se z bodu B pohybovala do bodu D, tzn. že vektor u a w by byly stejné. Během daného času se rychlost musela změnit o vektor z, který je rovnoběžný s úsečkou BS. Zde Newton použil své hypotézy, že přična změny rychlosti je ve Slunci a má tedy směr BS. Teprve výsledek vektorového součtu w + z je roven rychlosti v, jak plyne z rovnoběžníku EBDC.
Obsah trojúhelníků SAB a SBD je stejný, protože mají stejnou základnu SB a stejné výšky zpuštěné z bodů A a D (to plyne ze shodnosti trojúhelníků). Protože výška spuštěná z C je stejně velká jako výška spuštěná z D, mají i trojúhelníky SAB a SBC stejný obsah. Tímto postupem bychom pomocí eukleidovské geometrie dokázali shodnost obsahů ostatních trojúhelníků a tím i platnost II. Keplerova zákona.
K odvození Newtonova gravitačního zákona.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.
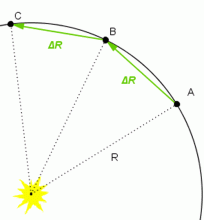
Předpokládejme, že se planety pohybují po kruhových drahách, což je speciální případ pohybu po elipse a hlavně je to velké matematické zjednodušení. Při tomto zjednodušení platí samozřejmě i třetí Keplerův zákon, kde se velikost hlavní poloosy změní na poloměr R. Na kružnici opět vyznačíme body A, B, C, které odpovídají polohám planety za stejný čas Δt, můžeme určit rychlost pohybu planety pomocí změny průvodiče ΔR
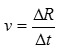
Pro velikost rychlosti také platí
![]()
kde T je doba oběhu. Při rovnoměrném pohybu po kružnici má planeta zrychlení
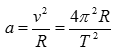
Podle třetího Keplerova zákona platí, že
![]()
a po dosazení máme
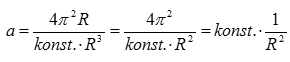
Síla působící na planetu o hmotnosti m je pak podle druhého Newtonova zákona
![]()
Slunce ale přitahuje planetu stejně velkou, ale opačnou silou
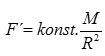
kde M je hmotnost Slunce.
Nyní již můžeme dokončit úvahy vedoucí ke konečnému vztahu pro sílu mezi planetami a Sluncem. Newton určitě nedával přednost jednomu tělesu před druhým. Proč by Slunce mělo mít výsadnější postavení než jakákoli z planet. Z toho důvodu začal předpokládat, že velikost síly mezi planetami je úměrná jak hmotnosti planety, tak hmotnosti Slunce. Obecný vzorec pro přitažlivou sílu mezi Sluncem a planetou
![]()
Ve skutečnosti je pohyb planet složitější. Kdyby existovala vedle Slunce jediná planeta, účinkem přitažlivých sil by se pohybovala jak planeta, tak i Slunce kolem společného těžiště v drahách sobě podobných.
