Archimedes

Archimedes.
Zdroj: Techmania Science Center. Autor: Pavel Trnka. Under Creative Commons.

Královská koruna

Asi nejznámější příběh o Archimedovi se do současnosti zachoval díky římskému architektovi Vitruviu Polliovi. Podle jeho vyprávění se kdysi syrakuský král Hierón II. obrátil na svého přítele Archimeda, aby mu pomohl vyřešit dilema, které měl se svým osobním zlatníkem. Panovník zlatníkovi předal kilogram zlata, aby z něj zhotovil korunu ve tvaru vavřínového věnce. Zlatník čile pracoval a za krátkou dobu vládci odevzdal překrásnou korunu, jejíž hmotnost odpovídala množství zlata, které od krále obdržel.

Panovník měl ale podezření, že klenotník část zlata při tavení nahradil levnějším kovem, třeba stříbrem nebo mědí. Chtěl se o počestnosti nebo naopak o hamižnosti zlatníka přesvědčit, aniž by korunu poničil. Obrátil se proto na přítele Archimeda. Archimedes přemýšlel, kudy chodil. Při návštěvě veřejných lázní si všiml, že se výška vodní hladiny v kádi měnila podle toho, jak moc se do ní nořil.

Tehdy prý Archimeda náhle napadlo řešení. Vyběhl nahý na ulici, namířil si to rovnou do královského paláce a přitom stále vykřikoval Heuréka! (Našel jsem!). Je asi dost možné, že tento příběh je vymyšlený, ale od té doby se řecké slovo heuréka používá na celém světě jako zvolání při náhlém a nečekaném objevu.

Archimedes v lázních.
Zdroj: commons.wikimedia.org. Public domain.

V lázních přišel Archimedes na to, že důležitá je nejen hmotnost tělesa, v tomto případě koruny, ale také její objem. K příběhu je nutné pro pořádek dodat, že zlatník byl nakonec popraven, protože královská koruna vytlačovala více vody, než by způsobilo stejné množství ryzího zlata.

Dílo

Archimedes ve své práci vycházel hlavně z Aristotela, Eukleida a Eratosthena. Eratosthenes si s Archimedem často dopisoval a navzájem diskutovali různé vědecké problémy. Archimedes se zabýval hlavně geometrií, konkrétně obvody a obsahy kruhů, obsahy rovinných útvarů ohraničených křivými čarami, objemy těles, povrchy těles, těžištěm těles a tečnami.

Archimedes napsal tato díla:

• O rovnováze neboli těžištích rovinných obrazců, kniha I. a II. Ve starověku se běžně používala páka, kladka, nakloněná rovina a kolo na hřídeli, ale teprve Archimedes matematicky popsal jejich princip. V díle je obsaženo několik postulátů o rovnováze na páce. Hlavními výsledky první knihy jsou věty o těžišti rovnoběžníku, trojúhelníku a lichoběžníku. Druhá kniha se věnuje těžišti parabolické úseče.
• O kvadratuře paraboly
• De mechanici propositionidus ad Eratosthenem methodus (Poselství Eratosthenovi o mechanické metodě řešení geometrických úloh), kde používal metody podobné infinitezimálnímu počtu. Spis byl objeven až v roce 1906.
• O kouli a válci, kniha I. a II. Velmi důležité výsledky týkající se výpočtů povrchů a objemů těles.
• O spirálách
• O konoidech a sféroidech. Věnuje se zde kuželosečkám a rotačním paraboloidům, hyperboloidům a elipsoidům. Jako první stanovil plochu elipsy. Stejně dobře zvládnul i výpočet objemu rotačního paraboloidu – tedy tělesa vzniklého rotací paraboly kolem její osy souměrnosti – a dále také rotačního elipsoidu a hyperboloidu.
• O plovoucích tělesech, kniha I. a II. V tomto traktátu je formulován a dokázán Archimedův zákon a rozebíráno plování těles.
• Měření kruhu. Z tého práce se dochovaly pouze tři matematické věty. V první je obsažen důležitý vztah mezi obvodem a obsahem kruhu – obsah kruhu je roven obsahu pravoúhlého trojúhelníka, jehož délky odvěsen jsou rovny poloměru a obvodu kruhu. Ve vztahu figuruje konstanta dnes označovaná jako π (poměr obvodu a průměru kruhu). Ve druhé a třetí větě pak uvádí odhady této konstanty.
• Počítání písku. V tomto díle se Archimedes zabýval slovním vyjádřením velkých čísel pomocí číselné soustavy, jejímž základem je oktáda (číslo 10⁸). Současně ukázal, že počet pískových  zrn, která by vyplnila celou sféru stálic, je nesrovnatelně menší než čísla, která jeho soustava popisuje. Tento spis je také jediné dílko, kde se Archimedes zabývá astronomickými otázkami, uspořádáním vesmíru a odhadem jeho velikosti.
• Kratochvíle
• Poučky. Drobný spis obsahující Archimedovy matematické výsledky.
• Problém dobytka

Archimedova díla se zachovala jen v arabských a jiných přepisech a překladech. Existuje ještě několik dalších prací, která se bohužel nedochovala. 

Portrét Archimeda od Domenica Fetti z roku 1620.
Zdroj: commons.wikimedia.org.

Výpočet čísla π

Archimeda fascinovalo číslo π – tedy poměr obvodu kruhu a jeho průměru. Snažil se ho určit co nejpřesněji, k tomu používal postup podobný integrálnímu počtu. Použil velmi zdlouhavou metodu (v době bez kalkulaček a jiných pomocníků). Vzal si dva mnohoúhelníky s 96 stranami, jeden vepsal kružnici a druhý opsal kružnici. Pak vypočítal velikosti stran obou mnohoúhelníků a zjistil jejich obvody. Diky tomu zjistil, že čislo π leží intervalu

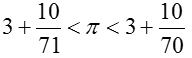
Po dosazení se tato hodnota pohybuje mezi 3,1408 < π < 3,1429. Bohužel se nikde neuvádí úplně přesný postup, jakým Archimedes k tomuto číslu dospěl.

Jednoduché stroje

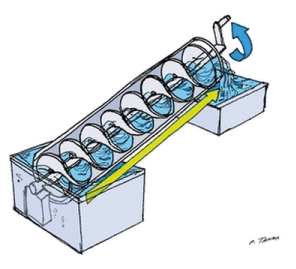
Ve fyzice se Archimedes zaměřil na výzkum statických sil, tj. sil které nevyvolávají pohyb. Zjistil podmínky rovnováhy a založil tak důležitou nauku o jednoduchých strojích. K tomuto zákonu se vztahuje další rčení, které se mu rovněž přisuzuje: „Dejte mi pevný bod a pohnu zeměkoulí“. Byl vůbec prvním vědcem zabývajícím se praktickým využitím teoretických poznatků. O svých technických vynálezech bohužel žádné pojednání nesepsal. Proto je těžké určit čeho je vlastně autorem. Zatímco kladka byla objevena už před Archimedem, kladkostroje poprvé pravděpodobně sestrojil on. Vedle kladkostroje vynalezl asi i soustavu převodů, šnekový převod a vodní šnek tzv. Archimedův šroub se šroubovou trubicí navinutou kolem osy, jejímž otáčením lze zdvíhat do malých výšek vodu. Tento vynález našel uplatnění v zavlažování a v dolech a v řadě zemí se užívá dodnes.

Archimedův šroub.
Zdroj: Techmania Science Center. Autor: Pavel Trnka. Under Creative Commons.

Obrana Syrakus

Když byly Syrakusy obléhány římskou armádou, dokázal Archimedes díky svým vynálezům bránit město celé dva roky. Střely z různých typů katapultů decimovaly římské legie, obrovské balvany zavěšené na jeřábech rozbíjely římské lodě, jiné galéry byly pomocí kladkostrojů zachyceny a převráceny jako skořápky. Soustavy zrcadel soustřeďovaly sluneční paprsky a zapalovaly nepřátelské lodě.

Nakonec Římané obránce Syrakus nechali vyhladovět a přece jen zvítězili. V roce 212 před n. l. město padlo. S pádem Syrakus je spojena i pověst o Archimedově smrti. Archimedes si prý jako obvykle nevšímal dění kolem sebe a byl zcela ponořený do svých geometrických úvah, ve kterých bádal nad kruhy nakreslenými v písku. Náhle se před ním objevil římský voják s vytaseným mečem a vyzval ho, aby jej následoval k jeho pánovi. Archimedes tehdy řekl: „Aposthéti, ó anthrópe, tú diagrammatos mú!“ (Nedotýkej se mých kruhů!). Řešil totiž právě daleko důležitější problém než otázky světovlády. Snažil se vypočítat plochu kruhové výseče. Popuzený a prchlivý voják učence bez milosti probodl.

Archimedova smrt na obraze Thomase Degeorga z roku 1815.
Zdroj: commons.wikimedia.org. Public domain.

Na Archimedův hrob byla položena deska s rytinou představující kouli ve válci, což byl objev, kterého si nejvíce cenil. Spočívá v tom, že sestrojíme–li kouli, obalíme–li ji těsně válcem a nakonec sestrojíme–li i kužel, který má stejnou základnu a výšku jako onen válec, jsou obsahy těchto těles v jednoduchém poměru 2:3:1.

Použité zdroje

[1] BEČVÁŘ, J. – ŠTOLL, I. Archimedes: největší vědec starověku. 1. vydání. Praha: Prometheus, 2005. 72s. ISBN 80–7196–273–2.

[2] BEČVÁŘOVÁ, M. Archimédovy práce česky. 29. mezinárodní konference Historie matematiky, Velké Meziříčí, 22. 8. – 26. 8. 2008, s. 93–102 1. vydání. Praha: Matfyzpress, 2008. ISBN 978-80-7378-048-7.

[3] LENARD, P. Velcí přírodozpytci. Přeložil F. X. Lánský. 2. české vydání. Praha: Vydavatelstvo Družstevní práce, 1943.

[4] Encyklopedická edice, listy, matematici. ISBN 80–860–44–05–X.