Družice se spolu se Zemí pohybují kolem Slunce, ale neúčastní se rotace Země. Proto pohyb umělé družice popisujeme vzhledem ke středu Země. Předpokládejme, že se družice pohybuje v takové výšce nad zemským povrchem, v níž je odpor vzduchu zanedbatelně malý. Pohyb družice vzhledem ke středu Země je ovlivňován jen gravitační silou, kterou je družice přitahována k Zemi.
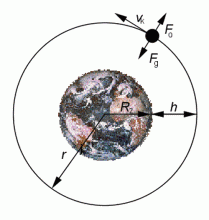
Pohyb družice na oběžné dráze.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.
Nejjednodušší trajektorií umělé družice je kružnice. Rychlost vk, kterou musíme družici ve výšce h nad povrchem Země udělit, aby konala rovnoměrný pohyb po kružnici o poloměru r, se nazývá kruhová rychlost. Je–li RZ poloměr Země, MZ hmotnost Země a m hmotnost družice, pak v gravitačním poli Země působí ve vzdálenosti r = RZ + h na družici gravitační síla, směřuje stále do středu Země, vytváří dostředivou sílu, která zakřivuje trajektorii družice. Obě síly jsou stejně velké, tedy Fd = Fg a po dosazení
![]()
a odtud po úpravě vztah pro velikost kruhové rychlosti
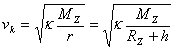
Vidíme, že velikost kruhové rychlosti nezávisí na hmotnosti družice, v dané výšce nad povrchem Země je pro všechna tělesa stejná. Velikost kruhové rychlosti klesá s rostoucí výškou nad povrchem Země. Je–li výška h velmi malá ve srovnání s poloměrem Země, můžeme ji ve vztahu pro velikost kruhové rychlosti zanedbat. Pro velikost kruhové rychlosti družice dostaneme výraz
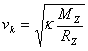
|
vzdálenost v poloměrech Země R |
kruhová rychlost (km/s) |
doba oběhu (h) |
|---|---|---|
|
1 |
7,9 |
1,4 |
|
2 |
5,6 |
3,96 |
|
6,6 |
3,1 |
24 |
|
10 |
2,5 |
44,4 |
|
60 |
1 |
27,2 |
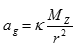
můžeme velikost kruhové rychlosti v blízkosti povrchu Země vyjádřit vztahem
![]()
Dosadíme ag = 9,81 m s–2 a vypočteme vk = 7,9 km s–1. Tato rychlost se nazývá první kosmická rychlost. Při dosažení této rychlosti obíhají družice okolo Země po kruhové dráze. Velikost první kosmické rychlosti závisí na hmotnosti planety.
|
Planeta |
kruhová rychlost |
Planeta |
kruhová rychlost |
|---|---|---|---|
|
Země |
7,91 km.s-1 |
Saturn |
36,96 km.s-1 |
|
Merkur |
3,94 km.s-1 |
Uran |
21,13 km.s-1 |
|
Venuše |
10,25 km.s-1 |
Neptun |
21,95 km.s-1 |
|
Mars |
5,03 km.s-1 |
Slunce |
611,50 km.s-1 |
|
Jupiter |
59,81 km.s-1 |
Měsíc |
3,94 km.s-1 |
Pohyb družic (umělých či měsíců) po kruhových trajektoriích kolem centrálního tělesa umožňuje také snadno určit hmotnost centrálního tělesa. Díky kruhovému pohybu oběžnice tak můžeme "zvážit" těleso jako je Slunce, Země a jiné planety.
Udělíme–li družici rychlost větší než je příslušná kruhová rychlost, změní se kruhová trajektorie družice na eliptickou. Elipsa má tím větší rozměry a je tím protáhlejší, čím je počáteční rychlost družice větší. Vzroste–li rychlost družice na hodnotu
![]()
nebo na hodnotu větší, změní se elipsa v parabolu, trajektorie již není uzavřená křivka, a družice se bude trvale vzdalovat od Země. Rychlost vp se nazývá druhá kosmická rychlost (11,2 km s–1).
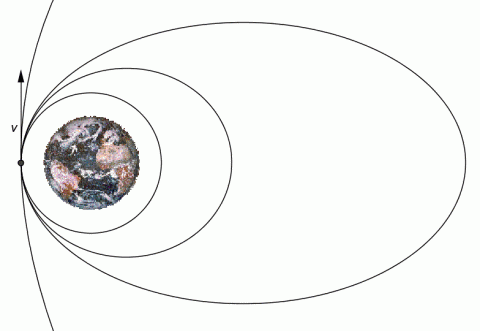
Kruhová, eliptická a parabolická dráha.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.
Předpokládali jsme, že gravitační pole Země je v prostoru osamoceno. Země je v gravitačním poli Slunce, a proto unikne–li družice z jejího působení, zůstává stále oběžnicí Slunce. Ledaže by počáteční rychlost byla tak velká, že by se rovnala únikové (parabolické) rychlosti pro gravitační pole Slunce ve vzdálenosti Země od Slunce. Nejprve ale určíme kruhovou rychlost Země kolem Slunce
![]()
a parabolickou rychlost
![]()
Tato hodnota se označuje jako třetí kosmická rychlost, nebo také úniková rychlost ze sluneční soustavy. Budeme–li chtít udělit tělesu takovou rychlost vzhledem ke Slunci, využijeme k tomu kruhovou rychlost Země kolem Slunce. Úniková rychlost by pak byla 42,1 – 29,8 = 12,3 km s–1.
S ohledem na gravitační pole Země musíme vypočítat únikovou rychlost v∞, kterou má těleso, když se dostane z vlivu tohoto pole. Jestliže uvažuje na začátku těleso, pak má kinetickou energii
![]()
a potenciální energii
![]()
(vzdalujeme–li se od Země, potenciální energie roste, proto záporné znaménko). Celková mechanická energie se přemění na kinetickou energii tělesa v nekonečnu a na potenciální energii, která je nulová. Zapíšeme–li vše do rovnice, dostaneme
![]()
Po úpravě a nahrazení
![]()
![]()
Můžeme určit rychlost v
![]()
Tato rychlost tedy představuje počáteční rychlost tělesa vzhledem k Zemi ve směru pohybu Země, kterou je nutno tomuto tělesu udělit, aby opustilo sluneční soustavu. Tato rychlost se označuje také jako třetí kosmická rychlost při využití rychlosti Země kolem Slunce.
Vhodné je startovat v určitých časových obdobích, která jsou nazývána startovacími okny, kdy jsou nároky na počáteční rychlost sondy minimální, tzv. Hohmannova dráha. Země a cílová planeta jsou pro tento let ve vhodné poloze jen v některých obdobích. Tato období se opakují např. pro Venuši po 584 dnech, pro Mars po 780 dnech.
