Málokdy existuje izolovaná soustava pouze dvou těles. Např. pohyb Měsíce kolem Země je ovlivňován i gravitačním účinkem Slunce a ostatních planet. Otázkou tedy je, zda vztahy a zákony odvozené v předchozích článcích jsou platné i pro tři tělesa, která na sebe navzájem gravitačně působí a tím se ovlivňují. I Isaaca Newtona tato myšlenka napadla a zjistil, že např. Měsíc v soustavě Země–Slunce působí velmi malé odchylky od Keplerových zákonů. Tyto odchylky se nazývají perturbace. Způsobují je buď málo hmotná blízká tělesa nebo velmi hmotná tělesa ve větší vzdálenosti. Je samozřejmé, že soustavu Země–Slunce nebudou ovlivňovat Jupiterovy měsíce. Nejvíce se perturbace objevují u komet. Když se kometa přiblíží příliš blízko k planetě, může její gravitační působení ovlivnit tvar její trajektorie.
Studium takových případů lze zahrnout do řešení problému n těles. K řešení je potřeba 3n diferenciálních rovnic druhého řádu. Pro problém 3 těles dostáváme 9 diferenciálních rovnic s 18 integracemi, ze kterých je řešitelných pouze 10. Z toho vyplývá, že problém tří těles je v nebeské mechanice obecně analyticky neřešitelný – nemůžeme určit tvar dráhy tělesa. Francouzský matematik Henri Poincaré totiž ukázal, že řešení obecného problému tří těles nelze vyjádřit pomocí známých elementárních funkcí. Proto se problém tří těles řeší většinou numericky (tj. přibližně). Na apletu si můžete vyzkoušet, jak složitou dráhu má planeta v soustavě dvou nehybných sluncí.
Nebeská mechanika umí řešit speciální případy. V roce 1772 Joseph Lagrange řešil problém tří těles v případě periodických pohybů, jestliže jedno z těles má nepatrnou hmotnost vzhledem k dvěma zbylým. Nalezl tak pět význačných bodů, které se nazývají librační (často také Lagrangeovy).
Pět libračních bodů.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.
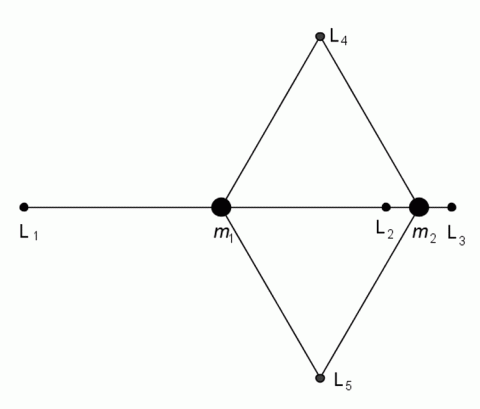
Librační body L1, L2 a L3 leží na spojnici obou těles a body L4 a L5 tvoří s oběma tělesy rovnostranné trojúhelníky. Librační body jsou místa, v nichž se vzájemné gravitační působení od obou těles vyrovnává s odstředivou silou, takže třetí těleso v nich umístěné je v „gravitační pasti“ a může tak zůstat v jejich blízkosti, aniž by se nějak změnila jeho dráha působením obou těles. Jejich poloha závisí pouze na hmotnosti obou těles. Librační body L1, L2 a L3 jsou nestabilní. Náraz meteoru, gravitační působení dalších planet, tlak fotonů apod. může způsobit vychýlení tělesa z libračního bodu. Objevil je už v roce 1750 Leonhard Euler, Lagrange objevil zbývající dva. Ty jsou stabilní, pokud je poměr hmotnosti obou těles přibližně 24,96. Např. pro dvojici Slunce-Jupiter se v blízkost těchto bodů nachází skupina planetek s označením Řekové a Trójani, u dvojice Saturn-Tethys se nachází malé měsíce Telesto a Calypso, u dvojice Saturn-Dione se v těchto bodech nachází malé měsíce Helene a Polydeuces. I když jsou body L1, L2 a L3 nestabilní, přesto lze v jejich blízkosti udržovat sondu s vynaložením jen velmi malého množství paliva. Do bodu L3 dvojice Země-Slunce bude vypuštěn teleskop Jamese Webba.
Použité zdroje:
[1] JELÍNEK, P. Řešení problému tří těles. JihoČAS, 1999 ročník 7. č. 3, s. 8–9.
[2] NĚMEC, J. Lagrangeovy librační body. Rozhledy matematicko–fyzikální, 1999, roč. 76, č. 1, s. 12–18. ISSN 0035–9343.
[3] SEYDLER, A. Historický rozvoj problemu tří těles. Časopis pro pěstování mathematiky a fysiky, 1886, roč. 15, s. 7–15, 65–70, 102–114.
