Již někteří řečtí učenci jako Anaxagoras nebo Diogenes měli dost jasnou představu o gravitaci. Na jejich myšlenky navázal Mikuláš Koperník, který ve svém díle De Revolutionibus Orbium Coelestum z roku 1543 píše: „Já však domnívám se, že není tíže ničím jiným, než přirozenou jakousi snahou vloženou v částice božskou prozřetelností Tvůrce veškerenstva, aby v jednotu a celek se spojily, nabývajíce tvaru koule. I jest pravdě podobno, že tato snaha i v Slunci, Měsíci a při jiných oběžnicích se nalézá, tak že jejím působením v tom kulatém tvaru, v němž se nám jeví, setrvávají, vykonávajíce při tom mnohými způsoby oběhy své.“ Galileo Galilei byl první, který objevil zákony volného pádu, a tím položil základní poznatky o tíze.
Johannes Kepler ve spise Astronomia nova z roku 1609 uvádí, že planety ovládá síla pocházející ze Slunce, že tato síla ovládá příliv a odliv. Neznal ale setrvačnost, a proto zavedl ještě tzv. tangenciální sílu přímo danou planetám. Snažil se také vysvětlit sílu gravitační pomocí magnetismu Slunce, zřejmě pod vlivem objevů Williama Gilberta. První kvantitativní krok k pochopení silového působení mezi planetami a Sluncem učinil Christian Huygens svými poznatky o odstředivé a dostředivé síle, která závisí na čtverci vzdálenosti tělesa od osy otáčení. Nabízela se tedy možnost, že i gravitační síla by mohla záviset na čtverci vzdálenosti tělesa. S touto myšlenkou přišli už v roce 1683 Robert Hooke, Edmund Halley a Christopher Wren. Žádný z nich ale nedokázal, že důsledkem je eliptická dráha planety, jak to plyne z I. Keplerova zákona. Robert Hooke tvrdil, že odpověď zná, ale úmyslně ji tají. Na podobném tématu pracoval delší dobu. V roce 1674 vydal spis An attempt to prove the motion of the earth, kde píše: „Každé těleso má svou tíhu, která se projevuje i mezi tělesy. Vržená tělesa se díky síle pohybují po elipse nebo kružnici. Tělesa se přitahují tím větší silou, čím jsou blíž.“ Bohužel se projevila Hookova neschopnost práci dokončit. Přesto si činil nemalé nároky na objev gravitačního zákona a ze žárlivosti rozběhl dost nechutný spor.
Edmond Halley důkaz neznal, ale vypravil se za Isaacem Newtonem, který na otázku, jaký tvar bude mít dráha planety, když velikost přitažlivé síly bude ubývat se čtvercem vzdálenosti, bez váhání odpověděl: „Bude to elipsa, vypočetl jsem to.“ Není divu, vždyť se problémem zabýval od roku 1666. V listopadu 1685 dostal Halley od Newtona devítistránkovou práci O pohybu těles na oběžné dráze.
Výsledkem celého sporu mezi Newtonovem a Hookem byl Newtonův objev závislosti přitažlivé síly na čtverci vzdálenosti. Bohužel výsledky nesouhlasily s pozorováním, a tak Newton váhal s publikováním. Roku 1679 zveřejnil Pierre Picard první přesné výsledky měření poledníkového stupně. Po přepočítání s novými údaji Newtona přepadlo takové rozčílení (i když byl flegmatik), že výpočty nemohl ani dokončit. Vždyť objevil univerzální přírodní zákon. Spor vyvrcholil tím, že Newton přiznal, že sám viděl ve fyzice dál jen proto, že stál na ramenech obrů. Isaac Newton zákon poprvé publikoval na silný popud Edmonda Halleyho v roce 1687 v samostatné kapitole svého díla Philosophiae naturalis principia mathematica.
Označení gravitace (z latinské gratis – těžký) se původně objevilo jako označení faktu – "snahy" či "touhy" živlu (a jejich směsí) najít střed Země. Newton odmítl hovořit o mechanismu či procesu interakce, když vyslovil svoji velkolepou domněnku, že totéž – ať už to funguje jakkoliv – co nutí jablko padat, váže i Měsíc k Zemi a planety ke Slunci. Navzdory kráse a eleganci obecné teorie relativity nemáme dodnes ověřenou teorii o "fungování" gravitace.
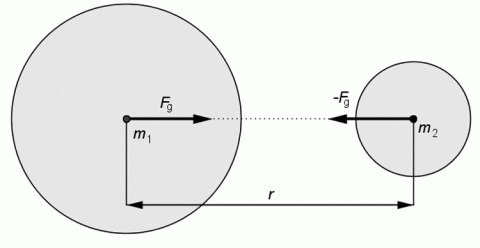
Gravitační působení dvou těles.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.
Dva hmotné body se přitahují vzájemně stejně velikými, ale opačnými silami. Velikost gravitačních sil je přímo úměrná součinu hmotností těchto bodů a nepřímo úměrná mocnině jejich vzdáleností.
![]()
Koeficient κ [kapa] = 6,67 · 10-11 N m2 kg2 je gravitační konstanta. Poprvé zákon ověřil v roce 1798 Henry Cavendish pomocí torzních vah, když se pokusil určit velikost gravitační konstanty.
Každé těleso vytváří v prostoru kolem sebe gravitační pole, které umožňuje gravitační působení sil mezi tělesy, která se vzájemně nedotýkají. Gravitační pole v okolí tělesa o hmotnosti M můžeme popsat pomocí intenzity gravitačního pole. Jako důsledky gravitačního působení mezi Zemí a Sluncem pozorujeme zakřivení trajektorie Země, mezi Zemí a Měsícem pozorujeme příliv a odliv.
![]()
Jednotkou intenzity gravitačního pole je N kg–1. Intenzita gravitačního pole je vektorová veličina, jejíž směr je shodný se směrem gravitační síly. Gravitační pole v okolí hmotného bodu se nazývá radiální gravitační pole. Ve všech bodech radiálního gravitačního pole, ležících v téže vzdálenosti r od hmotného bodu, má intenzita stejnou velikost. Protože intenzita směřuje ve všech místech k tělesu o hmotnosti M, nazývá se tento bod gravitační střed pole.
Podle gravitačního zákona přitahuje Země tělesa tak, jako by její hmota byla soustředěna v jejím středu, a přitom se velikost přitažlivé síly úměrně se čtvercem vzdálenosti zmenšuje. Co se ale stane, budeme–li těleso spouštět do nitra Země, tj. přibližovat je k středu naší planety? Tento problém vyřešil Newton pomocí slupkového teorému: Homogenní hmotná kulová slupka přitahuje vně ležící částici stejně, jako kdyby veškerá hmota slupky byla soustředěna v jejím středu. Podle tohoto teorému se gravitační síla při sestupu do nitra Země nezvětšuje, ale naopak zmenšuje. Lze to vysvětlit tím, že zemské částice působící přitažlivou silou nejsou už v takovém případě jen na jedné straně tělesa, ale obklopuji je. Závaží v hloubi Země je přitahováno dolů částicemi, které leží pod ním, současně však je taženo i vzhůru částicemi, která leží nad ním. Je možné dokázat, že zde vlastně působí jen přitažlivost koule, jejíž poloměr se rovná vzdálenosti tělesa od středu Země. Proto musí váha tělesa klesat tím rychleji, čím hlouběji do nitra Země sestupujeme. Ve středu Země ztratí těleso svou váhu docela, protože okolní částice je přitahují stejnou silou na všechny strany. Tíha tělesa je tedy teoreticky největší na zemském povrchu: vzdaluje–li se od zemského povrchu dolů nebo nahoru, jeho tíha by měla klesat. To by ovšem platilo, kdyby země měla stejnou hustotu. Ve skutečnosti hustota Země ke středu stoupá, takže při sestupu do nitra Země se přitažlivost z počátku ještě zvětšuje a teprve potom začíná klesat.
Newton zpětně odvodil z gravitačního zákona Keplerovy zákony. Třetí vyjádřil v přesném tvaru takto
![]()
kde doplnil hmotnost centrálního tělesa M a hmotnosti obou obíhajících těles m1, m2. Ty jsou velmi malé oproti M, a proto je můžeme zanedbat a vztah zapsat tak, jako Kepler
![]()
Použité zdroje:
[1] CHYTILOVÁ, M. Gravitační pole. Gravitační pole Země. Tíhová síla. Tíha tělesa. Běztížnost. Matematika a fyzika ve škole, červen 1983, roč. 13, č. 10, s. 680–690.
[2] KUBĚNA, J. O Newtonových a Keplerových zákonech aneb, jak asi Newton na své zákony přišel. Matematika Fyzika Informatika: časopis pro výuku na základních a středních školách, duben 1998, roč. 7, č. 7-8, s. 409-416, 472-482. ISSN 1210-1761.

