V Zürichu byl Schrödingerovým šéfem Peter Debye, který ho požádal, aby na téma de Broglieho vln a Bohrova modelu vypracoval přednášku. Schrödingerovi se do zpracování tématu moc nechtělo. Debye tedy využil svého postavení (naštěstí pro fyziku) a Schrödingerovi řekl, že přednášku udělat musí. Schrödinger předpokládal, že každou částici provází de Broglieho vlna, která může obíhat kolem jádra jen tehdy, je–li obvod dráhy celistvým násobkem vlnové délky. Tím bylo vysvětleno, proč nemůže elektron obíhat po libovolné dráze. Pro takovou vlnu musí platit nějaká vlnová rovnice, která bude relativistická a kvantová. Téměř na počkání rovnici vytvořil (dnes se nazývá Klein, Gordon, Fokova), avšak nedávala výsledky shodné s pozorováním spektra atomu vodíku. Formuloval i nerelativistickou kvantovou aproximaci (dnes se nazývá Schrödingerova rovnice), která vedla ke skvělým výsledkům. Přednáška byla pečlivě vyslechnuta a pak ji ředitel ústavu zhodnotil: „člověče, vždyť vy jste našel nový princip vlnové mechaniky“. Vše publikoval v roce 1926 v sérii článků uveřejněných v Annalen der Physik. Za tyto práce byl v roce 1933 vyznamenán Nobelovou cenou za fyziku a ta mu pomohla získat místo v Magdalen College v Oxfordu.
Postupujme tedy stejně jako Schrödinger. Nejprve prozkoumáme vlnové chování elektronu na dráze kolem atomového jádra vodíku. De Broglieho vlnová délka elektronu je
![]()
a jeho rychlost podle Rutherforodova modelu
![]()
a spojením obou vzorců získáme pro vlnovou délku
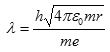
Dosazením základních konstant získáme vlnovou délku de Broglieho vlny elektronu
![]()
Tato hodnota přesně odpovídá obvodu elektronové dráhy při poloměru r = 5,3 · 10–11 m, který vypočetl již Rutherford. Dráha elektronu v atomu vodíku odpovídá délce jedné celé elektronové vlny, která navazuje sama na sebe.

Souvislost de Broglieho vln a dráhy elektronu.
Zdroj: commons.wikimedia.org. Autor: Pieter Kuiper. Public domain.
Na základě této úvahy můžeme říci, že elektron může kroužit kolem jádra nekonečně dlouho aniž by vyzařoval energii za předpokladu, že jeho dráha obsahuje celočíselný počet de Broglieho vlnových délek. Tento postulát kombinuje částicovou i vlnovou povahu elektronu. Pro vlnovou délku můžeme napsat následující podmínku
![]()
Kde rn představuje poloměr dráhy, který obsahuje n vlnových délek. Celé číslo n se nazývá kvantové číslo dráhy. Jestliže dosadíme za vlnovou délku z předchozího vztahu
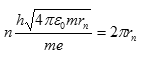
Tak po úpravě obdržíme Bohrův poloměr vodíkového atomu
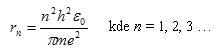
Různé dovolené dráhy znamenají různé energie elektronu. Energie elektronu určená pomocí orbitálního poloměru rn, která vychází z Rutherfordových výpočtů
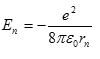
a po dosazení Bohrova poloměru
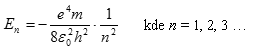
zkráceně
![]()
Energie dané tímto vztahem se nazývají energetické hladiny vodíkového atomu. Tyto energie jsou všechny záporné, tzn. že elektron nemá dostatek energie, aby unikl z atomu. Ze vztahu je patrné, že hodnoty energie En se mění skokem a nikoli spojitě.
