Při deformování drátu tahem se drát prodlouží z původní délky l0 o délku Δl. Tato veličina se nazývá prodloužení. Prodloužení je přímo úměrné velikosti síly F, která na drát působí; počáteční délce l0; materiálu drátu a nepřímo úměrné průřezu S. Odtud vyplývá vztah
![]()
kde k je konstanta úměrnosti závislá na pružných vlastnostech materiálu. Vztah můžeme přepsat do tvaru
![]()
konstanta E se nazývá modul pružnosti v tahu – nebo také Youngův modul (jednotka pascal). Je to takové myšlené napětí, které by způsobilo prodloužení drátu o celou původní délku. Moduly pružnosti kovů s rostoucí teplotou klesají. Hodnoty modulu pružnosti pro různé pevné látky jsou uvedeny v MFChT. Podíl
![]()
se nazývá relativní prodloužení a druhý podíl
![]()
se nazývá normálové napětí (jednotka pascal). Po dosazení těchto veličin do původního vztahu dostaneme
![]()
Normálové napětí je přímo úměrné relativnímu prodloužení. Tento poznatek publikoval anglický fyzik Robert Hooke v roce 1676 výrokem „Ut tensio, sic vis.“ (Napětí jest úměrno deformaci.). Podle něho se nazývá Hookův zákon. Hookův zákon má velký význam v technice a ve stavebnictví. Jestliže do vztahu dosadíme sílu působící opačným směrem, získáme stejný vztah pro deformaci tlakem. Prodloužení nám také vyjde záporné, jedná se totiž o zkrácení.
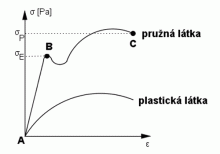
Během namáhání tahem dochází k prodlužování tělesa ve směru působící síly. Zároveň dochází k jeho ztenčování ve směru kolmém. Proto při určité působící síle může dojít k přetržení drátu. Jestliže závislost napětí na prodloužení skutečné tyče vyneseme do grafu, získáme tuto křivku
Přímka AB znázorňuje obor platnosti Hookova zákona. Bod B se nazývá mez pružnosti (mez elasticity v tahu) a těleso je až do této chvíle deformováno elasticky. V roce 1906 bylo na mezinárodním kongresu v Bruselu usneseno, že mezí pružnosti se rozumí trvalé prodloužení menší než 0,001 % původní délky. Od bodu B nastává deformace trvalá a již při malém zatížení prodloužení materiálu zprudka roste – říkáme, že materiál teče. Bod C představuje mez pevnosti – okamžik, kdy se těleso přetrhne. K přesnému určení meze pružnosti i pevnosti se používá trhací stroj a zkušební tyče ze zkoumaného materiálu. Podle tvaru grafu lze rozhodnout, která látka je pružná, která křehká či schopná značných plastických deformací. V praxi se častěji používají hodnoty tzv. dovoleného napětí. Je to maximální v praxi přípustná hodnota normálového napětí při deformaci tahem nebo tlakem. Jeho hodnota se volí značně menší, než je mez pevnosti.
Podobně jako Yonghův modul pružnosti E pro deformaci tahem, můžeme zavést i moduly pružnosti v tlaku K a modul pružnosti ve smyku G.
|
Látka |
E (∙1010 Pa) |
G (∙1010 Pa) |
K (∙1010 Pa) |
|---|---|---|---|
|
hliník |
7,07 |
2,64 |
7,3 |
|
křemík |
9,5 |
3,3 |
31,3 |
|
měď |
12,3 |
4,55 |
13,8 |
|
olovo |
1,6 |
0,56 |
4,3 |
|
platina |
17,0 |
6,1 |
25,6 |
|
stříbro |
7,9 |
2,9 |
10,1 |
|
zlato |
7,85 |
2,76 |
16,7 |
|
železo |
21,2 |
8,2 |
17,2 |
|
uhlík |
18,0 |
7,2 |
12,0 |
|
diamant |
112.0 |
52,0 |
43,5 |
|
bronz |
9,7–10,2 |
3,3–3,7 |
11,2 |
|
dural |
7,25 |
2,75 |
7,5 |
|
litina |
11,0 |
4,4 |
7,3 |
|
mosaz |
9,9 |
3,65 |
11,8 |
|
ocel |
20,4 |
7,9 |
16,1 |
|
SiO2 |
7,3 |
3,1 |
3,7 |
|
kaučuk |
0,00015 |
0,00005 |
0,0083 |
|
polystyren |
0,32 |
0,12 |
0,31 |
|
sklo |
5 – 6 |
2 – 2,5 |
3,8 – 3,6 |
|
plexisklo |
0,33 |
0,12 |
0,37 |
|
H2O led |
0,93 |
0,35 |
0,91 |
|
NaCl |
3,85 |
1,52 |
2,5 |
Moduly pružnosti a zejména jejich závislosti na různých parametrech (např. na teplotě) má velký význam pro fyziku materiálů – vypovídají mnohé zejména o vazebních silách mezi atomy v pevných látkách.