německý fyzik a snad největší matematik vůbec
„V teorii čísel se velmi často stává, že díky jakési neočekávané šťastné náhodě vznikají nádherné nové poznatky pomocí indukce.“
Johann Karl Friedrich Gauss se narodil v Braunschweigu a byl jedináčkem v rodině Gerharda Dietricha a Dorothey Gaussových. Jeho máma pracovala jako služka, neměla žádné vzdělání, neuměla psát a číst uměla jen málo. Jeho táta byl muž mnoha řemesel, pracoval jako metař, zahradník, zedník apod. Jako malý kluk se Karl učil dřív počítat než mluvit. Pak začal své známé a příbuzné "prosit o písmena", a najednou uměl číst, aniž by kdokoli věděl, jak k tomu vlastně přišel.

Karl Friedrich Gauss.
Zdroj: commons.wikimedia.org. Autor: Siegfried Detlev Bendixen, 1828. Public domain.
První roky matematického génia
Když byly Karlovi tři roky, poslouchal jednou, jak jeho otec počítá výplaty pro dělníky. K velikému překvapení všech přítomných tříletý klučina svého otce opravil a hned řekl správný výsledek. Otec mzdu znovu přepočítal a zjistil, že chlapec má skutečně pravdu. V sedmi letech začal chodit do školy, kde měl ve třídě sto spolužáků, ale nijak mezi nimi nevynikal.
Teprve v devíti letech na sebe upozornil příhodou, která se dodnes traduje všude, kde je řeč o Gaussovi. Stalo se, že učitel Büttner v Gaussově třídě chtěl mít hodinu klid, a proto uložil žákům, aby sečetli všechna čísla od jedné do šedesáti. Kdo byl s úlohou hotov měl položit břidlicovou tabulku na veliký stůl, hezky jednu na druhou, aby učitel mohl kontrolovat, v jakém sledu žáci úlohu odevzdávali.
Po krátké chvilce vyskočil žáček Gauss a položil svou tabulku na stůl. Učitel držel v ruce rákosku a soucitně pohlížel na bledého uličníka. Pokládal chlapce za vykutáleného vtipálka, ale v tuto chvíli se rozhodl ho ještě nechat na pokoji, aby nerušil ostatní. Když už všichni odevzdali svá řešení, prohlédl jedno po druhém. Na první tabulku úplně vespod skoro zapomněl. Když ji vzal do ruky, tak ke svému úžasu uviděl, že je na ní číslo 1830. A to je správný výsledek.
Malý Karl vše vysvětlil jako naprostou samozřejmost, že výsledek součtu všech čísel od jedné do šedesáti se dá říct ihned zpaměti. Není třeba sčítat jedno číslo po druhém tak, jak to dělali ostatní. On si sečetl první číslo s číslem posledním – vyjde 61. To pak stačí vynásobit počtem párů čísel v úloze, tj. třiceti. A třicetkrát jednašedesát je 1830. Když to učitel slyšel, opatřil pro malého Gausse učebnici matematiky až z Hamburku a jeho pomocník Bartels (později profesor matematiky na univerzitě v Kazani a Dorpatu) začal s Gaussem studovat vyšší matematiku.
V době, kdy jeho spolužáci sotva zvládali násobilku, Gauss už ovládal nekonečné řady a infinitezimální počet. Když už ho ani učitel Büttner neměl co naučit, tak Gauss v roce 1788 nastoupil na místní gymnázium a rovnou do druhého ročníku. Gaussovy vynikající schopnosti zaujaly Carla Wilhelma Ferdinanda, braunschweigského vévodu, který se rozhodl nadaného mladíka podporovat. V roce 1792 Gauss nastoupil na brunšvickou akademii Collegia Carolina, kde se seznámil s pracemi Isaaca Newtona, Josepha Lagrange a Leonharda Eulera.
Na univerzitě
Roku 1795 Gauss nastoupil na univerzitu v Göttingenu, kde se věnoval studiu klasické filologie. Na matematiku nezapomněl. 30. března 1796 dokázal, že lze sestrojit pravítkem a kružítkem pravidelný sedmnáctiúhelník jako důsledek nově zbudované teorie dělení kruhu. Ukázal, že tímto způsobem lze sestrojit pouze ty pravidelné mnohoúhelníky s lichým počtem stran, jejichž počet stran je násobkem prvočísel 3, 5, 17, 257 nebo 65 537. Jeho nejdůvěrnějším přítelem byl v této době Farkas Bolyai von Bolya (později otec Jánose Bolyaie).
Roku 1798 Gauss dokončil univerzitní studia a odešel do Braunschweigu, aby se připravoval na doktorát z filozofie (v Německu považovaný za ukončení univerzitního studia). Roku 1799 předložil matematickou disertační práci na univerzitě v Helmstedtu a na základě své disertační práce byl bez zkoušky promován na doktora. Jeho disertační práce se zabývala rozborem základních algebraických teorémů. Mimo jiné zde dokázal, že každá algebraická rovnice má alespoň jeden kořen. Už ve třiadvaceti letech se stal dopisujícím členem petrohradské Akademie.
V roce 1801 vyšla Gaussova kniha Disquisitones aritmeticae (Pojednání o aritmetice), která obsahuje 7 částí. Poslední část se zabývá teorií čísel, kde Gauss zformuloval teorém o tom, že každé přirozené číslo se dá zapsat jako součin prvočísel. Ke Gaussově škodě se velká část nákladu ztratila a tak se jeho myšlenky dostaly jen k malému okruhu čtenářů.
Planetky
Gauss však nebyl jen matematik. Zabýval se optikou, působil jako zeměměřič a podílel se na tvorbě map. Významně zasáhl i do astronomie. 1. ledna 1801 astronom Giuseppe Piazzi v Palermě objevilv mezeře mezi Marsem a Jupiterem novou zajímavou planetku Ceres. Planetka se ale astronomům při přechodu přes sluneční kotouč ztratila.
Gauss vypracoval na základě tří Piazzových pozorování z 2. a 22. ledna a 11. února úplně novou metodu nejmenších čtverců pro výpočet dráhy nebeských těles. 7. prosince stejného roku ji astronom Zach Ceres znovu nalezl přesně tam, kde Gauss její polohu předpověděl. Ve stejném roce si mohl svou metodu ověřit ještě na planetce Pallas. Sláva Gaussovi přinesla nabídku na ředitelské místo v petrohradské hvězdárně. On však odmítl, protože mu lépe vyhovovala nezávislost a renta, kterou mu poskytoval vévoda.
V říjnu 1805 se Gauss oženil s Johannou Osthofovou a o rok později se jim narodil syn Joseph. V roce 1806 byl v napoleonských válkách smrtelně zraněný vévoda z Braunschweigu a Gauss tak ztratil materiální podporu. Přijal proto nabídku na místo ředitele rozestavěné göttingenské hvězdárny.
28. března 1809 vydal spis Theoria motus corporum coelestium, in sectionibus conicis circa solem ambientium, auctore Carolo Friderico Gauss (Teorie pohybu nebeských těles), kde poprvé publikoval svou teorii nejmenších čtverců a výsledky výpočtů drah planet. Netrvalo dlouho a z Gausse se stal slavný vědec.
Úspěšný pracovní život mu zakalila smutná rodinná událost. Po porodu třetího dítěte onemocněla Gaussova manželka Johanna a 11. října 1809 zemřela. Ne na dlouho osiřely tři Gaussovy děti, protože si v roce 1810 vzal Minnu Waldeckovou, dobrou přítelkyni své zesnulé manželky. Minna bohužel v roce 1831 zemřela také.
Napoleonské války protahovaly stavbu göttingenské hvězdárny. Teprve na podzim roku 1816 dostal Gauss služební byt. Dobové prameny neuvádí žádného jiného zaměstnance, a proto zřejmě Gauss prováděl všechna pozorování sám.
Základy geodezie
Již od mládí se Gauss zabýval astronomickým pozorováním, což souviselo i se zeměměřičskými postupy a přístroji. Poprvé se se zeměměřičstvím setkal už v roce 1802, když se zúčastnil měření v německém Harcu. V roce 1820 ho hannoverský král pověřil, aby vykonal geodetická měření hannoverského království. Jednalo se hlavně o určení délky části poledníku. Už při prvních měřeních odhalil nedostatky tehdejší geodezie a aby potlačil chyby vzniklé nepřesností měřidel zavedl i zde metodu nejmenších čtverců. Kromě toho do geodezie zavedl používání heliotropu (sloužil k vysílání světelných sigálů na velké vzdálenosti), vypracoval síť trojúhelníků a teorii podobného zobrazení.
Z počátku prováděl měření sám jen s pomocí syna Josepha. Později byli měřením pověřeni důstojníci hannoverské armády. Zpracováním trigonometrických souřadnic více než 2500 bodů zpracoval víc než milion údajů, které dokončil až v roce 1848. Jeho geodetické dílo je shrnuto v Disquisitiones Generales circa super ficies curvas.
Magnetismus
Během svého působení v roli ředitele göttingenské hvězdárny podnikl Gauss jen několik cest. Pro jeho další práci byla důležitá cesta v roce 1828 do Berlína na zasedání německých přírodovědců. Zde se seznámil s mladičkým Wilhelmem Weberem, který se v roce 1831 do Göttingenu přistěhoval, aby tam působil jako profesor fyziky. Gauss se do té doby věnoval fyzice jen málo. Společně s Weberem zavedli absolutní elektromagnetickou soustavu jednotek (cm–g–s) a po roce spolupráce přišli na teorii zemského magnetismu, kterou publikovali v Intensita vis magneticae terrestris ad mensuram absolutam revocata (Intenzita zemského magnetismu, uvedená na absolutní míru).
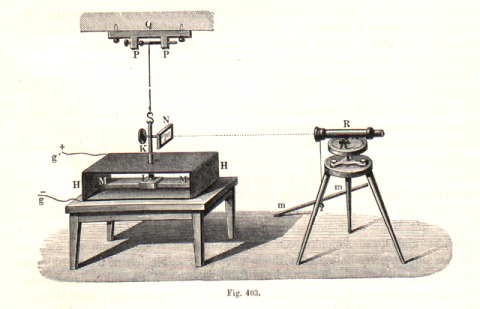
V roce 1833 byla dokončená stavba Gaussovy magnetické laboratoře, kde nebyl použitý žádný magnetický kov. Spolu s Weberem sestrojili první primitivní telegraf, pomocí kterého mohli přenášet zprávy na vzdálenost asi 1,5 km. Telegraf spojoval fyzikální kabinet göttingenské univerzity s hvězdárnou. Fungoval bezchybně až do roku 1845, kdy ho zničil blesk. Gauss ještě publikoval atlas magnetismu, vydával časopis Magnetické rozhledy, ve kterém otiskoval výsledky svých výzkumů a společně s Weberem založil magnetický spolek. Jenže Weber se dostal do politických sporů, v roce 1837 byl propuštěn a v roce 1840 přijal místo profesora na lipské univerzitě. V roce 1839 Gauss po několika letech usilovné práce uveřejnil spis Algemeine Theorie des Erdmagnetismus (Všeobecná teorie zemského magnetismu), kde na základě svých výpočtů uvedl, že geografické a magnetické póly Země se nekryjí (tento poznatek byl později expedicemi plně potvrzen). Pomocí Royal Society a vědců téměř z celé Evropy zahájil měření magnetického pole Země. Z naměřených údajů zjistil souvislosti mezi změnami magnetického pole Země, výskytem polárních září a změnami ve sluneční činnosti.
Matematika
Těžko bychom hledali byť i jen jedinou oblast matematiky, kterou by Gauss nějak neovlivnil. Jeho největší láskou byla teorie čísel, intenzivně se zabýval i statistikou a počtem pravděpodobnosti. Základní rozložení pravděpodobnosti dodnes znázorňujeme Gaussovou křivkou. Vypracoval algebru a aritmetiku komplexních čísel a novou teorii prvočísel, v níž 3 je prvočíslo, ne však 5 neboť: 5 = (1 + 2i)∙(1 − 2i), komplexní čísla vyjádřil jako body v rovině. Jeho práce z klasické geometrie znamenaly první významný pokrok v geometrii od dob antických Řeků. Z našeho dnešního hlediska je však nejdůležitější skutečnost, že Gauss na konci 18. století objevil zcela nový typ geometrie, která se od té klasické, euklidovské zásadně liší. Eukleidova geometrie je založena na pěti základních poučkách, tzv. axiomech. Po dva tisíce let nikdo z matematiků nedokázal na Euklidově systému axiomů nic opravit ani vylepšit. Avšak Gauss ke svému největšímu překvapení zjistil, že změnou pátého axiomu vznikne úplně nový systém – geometrie zakřiveného prostoru! Tento objev byl tak odvážný, že se mladý Gauss polekal a raději ho ani nezveřejnil, ani nepodpořil snahy Nikolaje Lobačevského a Jánose Bolyaie o její prosazení. Později rozvinul neeuklidovskou geometrii Gaussův žák Bernhard Riemann a ve 20. století jedině díky tomu mohl Albert Einstein vytvořit obecnou teorii relativity.
V roce 1848 se do Göttingenu vrátil Gaussův spolupracovník Weber a jeho asistentem se stal velice nadaný mladík Bernhard Riemann. Gaussovou poslední významnou akcí, které se účastnil, bylo otevření železniční trati mezi Hannoverem a Göttingen. Teprve v roce 1854 ve věku 77 let, když stále působil jako ředitel göttingenské hvězdárny, začal pociťovat důsledky svého věku a jeho stav se stále zhoršoval. Ráno 23. února 1855 zemřel ve spánku. Jak se později z jeho poznámek ještě zjistilo, měl rozpracovány ještě desítky zajímavých poznatků, které nikdy nepublikoval a na kterých si založili slávu jiní vědci v pozdější době.
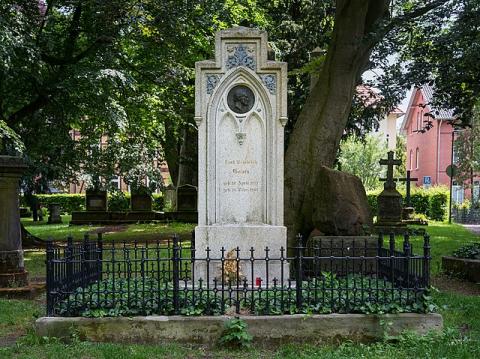
Hrob Karla Gausse na hřbitově v Göttingen.
Zdroj: commons.wikimedia.org. Autor: Julian Herzog. Under Creative Commons Attribution 4.0.
Něco málo o Gaussově osobě
Již rok po Gaussově smrti vyšla jeho první biografie, kterou vydal jeho přítel, göttingenský profesor mineralogie a geologie Sartori von Walterhausen, kde např. praví: “Gauss byl člověk železného charakteru, který uměl ocenit jen silné povahy; všechna nestálost, nerozhodnost v životních cílech, všechna polovičatost tolika lidí mu byla veskrze protivná. Jeho vlastní, všem ostatním záměrům čelící životní plán tkvěl ve ztělesnění jeho velkých vědeckých ideí, ve vytrvalém snažení dovést exaktní vědy 19. století k novému rozkvětu, k nové dokonalosti. Zatímco každý jiný smysl existence se mu zdál podřadný, sledoval svůj cíl s nepopsatelnou energií. Při prosazování této velké úlohy byl podněcován takovou usilovností vůle a činorodosti, jaká by se v této podobě jen velice zřídka mohla přisoudit smrtelníku; mohl proto zvládnout v poměrně krátké době skutečně herkulovské dílo. Vnitřní vazby těchto zvláštních nadání spolu s božským geniem a téměř až do posledních let pevným zdravím přinesly onu obdivuhodnou tvorbu, již naše století uznalo a která bude budoucností vděčně uctívána.“ [7] Gauss byl starostlivým otcem, zaznamenával vše, co se událo v jeho rodině – první zoubky svých dětí apod. Zásadně nenosil vyznamenání, kterými ho různí vládci a potentáti zahrnovali.
Zdroj: commons.wikimedia.org. Public domain.
Při uveřejňování své práce se řídil heslem „pauca sed matura“ (málo avšak dokonale). Pozdější bádání v jeho pozůstalosti a především v deníku, který si celý život vedl, přineslo obraz matematika, který zasáhl téměř do všech oblastí tehdejší matematiky.
Ke konci života měl Gauss dva žáky Bernharda Riemanna a Richarda Dedekinda. Druhý jmenovaný o Gaussovi napsal: “Gauss nosil lehkou černou čapku, dosti dlouhý hnědý svrchník, šedé kalhoty. Sedával většinou klidně, poněkud skloněn hleděl před sebe s rukama svěšenýma podél těla. Mluvil zcela volně, velice zřetelně, jednoduše a prostě. Když však chtěl zdůraznit určité nové hledisko, k čemuž potřeboval zvlášť charakteristický výraz, pozvedl téměř okamžitě hlavu, obrátil se ke svému sousedu a pohlížel naň během důrazné řeči živě svýma krásnýma pronikavě modrýma očima. To bylo nezapomenutelné … Jestliže přecházel od zásadního objasnění k odvozování matematických vzorců, pozvedl se a ve státnickém, zcela vzpřímeném postoji psal na tabuli za ním stojící svým osobitým rukopisem, přičemž se mu díky šetrnosti a účelnému uspořádání vždy podařilo vystačit se sebemenším prostorem na ní. Pro číselné příklady, na jejichž pečlivé provedení kladl mimořádný důraz, si přinášel potřebné údaje na malých lístcích.“ [7]
Použité zdroje
[1] BOREC, T. Dobrý den, pane Ampére. 1. vydání. Praha: Státní pedagogické nakladatelství, 1980. ISBN 14–031–81.
[2] HOBST, E. – HOBST, M. Carl Friedrich Gauss – zakladatel´modernej matematiky. Pokroky matematiky, fyziky a astronomie, 2007, roč. 52, č. 4, s. 296-307. ISSN 0032-2423.
[3] LAVIČKOVÁ, M. Carl Friedrich Gauss. Přemožitelé času 5.
[4] LENARD, P. Velcí přírodozpytci. Přeložil F. X. Lánský. 2. české vydání. Praha: Vydavatelstvo Družstevní práce, 1943.
[5] MALÍŠEK, V. Karl Friedrich Gauss a jeho zásluhy o rozvoj exaktních věd. Matematika a fyzika ve škole, duben 1977, roč. 7, č. 8, s. 581–584.
[6] STUDNIČKA, F. J. Karel Bedřich Gauss. Na oslavu stoleté památky jeho narození. Časopis pro pěstování mathematiky a fysiky, 1877, roč. 6, s. 145–196.
[7] WISSING, H. Karl Friedrich Gauss. Pokroky matematiky, fyziky a astronomie, 1977, roč. 22, č. 4, s. 195-204. ISSN 0032-2423.
[8] Historie elektřiny a magnetizmu. Konstrukční elektronika A RADIO, 2003, č. 5.