Jestliže na těleso působí více sil, je potřeba vědět jakým směrem bude působit výsledná síla. Skládat síly působící na tuhé těleso tedy znamená nahradit tyto síly jedinou sílou, která má na těleso stejné účinky jako skládané síly. Tato síla se nazývá výslednice sil. Výslednice jako každá jiná síla je určena svou velikostí, směrem a působištěm.
Síly působící v jednom bodě
Působí–li na těleso dvě síly F1, F2 stejného směru působící v jednom bodě je velikost jejich výslednice F rovna součtu velikostí obou sil
Jako příklad si můžeme představit pohádku o řepě, kde ani síla dědka, babky, vnuka, vnučky, psa a kočky nestačila na vytáhnutí řepy. Až malá myší síla pomohla.
Skládání sil stejného směru.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.
Velikost výslednice dvou sil působících v jednom bodě v opačném směru je rovna rozdílu velikostí obou skládaných sil
a má směr shodný se směrem větší síly. Jako příklad si můžeme představit siláky přetahující se o lano.
Skládání sil opačného směru.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.
Ke skládání sil různého směru působících v jednom bodě využijeme tzv. rovnoběžník sil. Tento princip vyslovil pro kolmé síly částečně Galileo Galilei a Simon Stevin a zobecnil jej Isaac Newton v roce 1687 ve svých Principiích. Simon Stevin vyslovil větu, že tři síly jsou v rovnováze, mají–li se k sobě jako strany trojúhelníka pravoúhlého.
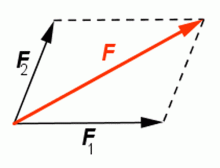
Skládání sil různého směru.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.
Působí–li na těleso více sil v jednom bodě, připojujeme postupně jednu sílu k druhé a zachováváme přitom jejich směr a velikost. Získáme silový mnohoúhelník, který může obecně být prostorový. Výslednice F
je určena vektorem, který mnohoúhelník uzavírá. Mnohoúhelník sil platí pro síly působící v rovině i v prostoru.
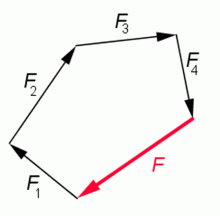
Skládání více sil různého směru.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.
Zvláštní případ nastává, jestliže po složení všech sil dojdeme do výchozího bodu. Výsledná síla je pak nulová a působící síly se navzájem ruší – jsou v rovnováze.
Síly působící v různých bodech tělesa
Uvažujme dvě síly působící na těleso v různých bodech, jak ukazuje obrázek.
Skládání sil působících v různých bodech tělesa.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.
Kdybychom takto působili na drát, napínali bychom ho, dokonce bychom ho mohli přetrhnout, zkrátka bychom ho deformovali. Podrobně o tom pojednávají další články.
Kdybychom uvažovali těleso, které se vlivem sil nedeformuje – tuhé těleso – pak můžeme použít úvahy z předchozí kapitoly a sílu –F přenést do působiště B a obě síly složit.
Síly působící na různá tělesa v prostoru
Jestliže působí více sil v různých bodech, pak výslednou silou je závěrná strana složkového mnohoúhelníku se šipkou proti sledu šipek daných sil a její polohu určuje průsečík krajních vláken vláknového mnohoúhelníku. Soustava různoběžných sil je v rovnováze, tvoří–li složkový mnohoúhelník se šipkami sil v jednom sledu uzavřený vláknový mnohoúhelník. Jak to provedeme? K tomu nám pomůže následující příklad. Mějme lanka napnutá tak, jak ukazuje obrázek. Soustava sil je v klidu, a tedy i v rovnováze. V uzlu 1 je soustava sil v klidu, síly se navzájem ruší. Podobně je tomu i v uzlech 2 a 3. Silové trojúhelníky mají vždy jednu sílu společnou, proto je můžeme zakreslit v jeden obrazec. Síly mezi uzly se navzájem ruší a ze všech sil zbývají jen krajní síly. Výslednicí krajních sil P1 a P2 je síla F, která je zároveň opačná k výslednicí sil F1 až F3.
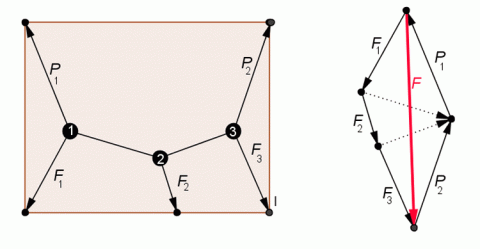
Skládání sil působících na růrzná tělesa v prostoru.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.
Rozkládání sil
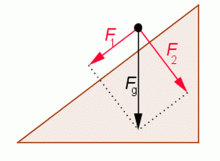
Často potřebujeme rozložit sílu, působící na těleso, na dvě složky. Nesou–li dva lidé zabitého kance na tyči, kterou drží každý z nich na jednom konci, rozložíme tíhu kance na dvě rovnoběžné složky, jejichž působiště je v místech, kde lidé tyč drží. Při sledování pohybu tělesa po nakloněné rovině rozkládáme tíhovou sílu na dvě různoběžné navzájem kolmé složky, z nichž jedna má směr rovnoběžný s nakloněnou rovinou, druhá je k nakloněné rovině kolmá.
Rozkládání sil.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.
Při rozkládání síly na dvě složky (nebo i více složek) platí stejná pravidla jako při skládání sil. Rozkládáme–li sílu na dvě různoběžné složky, volíme zpravidla směry, do nichž chceme sílu rozložit, a určujeme velikosti složek.
