Země není ve vesmíru nehybná, ale vykonává několik pohybů: rotace kolem osy za jeden den, oběh kolem Slunce za jeden rok, precesi a nutaci, měsíční pohyb kolem gravitačního středu dvojice Země-Měsíc, změny v naklonění rotační osy vzhledem k ekliptice, změny výstřednosti zemské dráhy, stáčení periapsidy, perturbace způsobené ostatními planetami a posouvání gravitačního středu Sluneční soustavy.
První představa o pohybech Země pochází od Herakleida, Platónova žáka, který Zemi přisoudil otáčivý pohyb kolem osy jednou za 24 hodin. Důkaz o tomto pohybu navrhl Royal Society Isaac Newton roku 1679. Kámen, který by padal z velké výšky k zemi, by nepadal kolmo, ale odchýlil by se k východu. K největšímu odklonu by došlo na rovníku a k žádnému na pólech. Royal Society svěřila pokusy Robertu Hookovi, sekretáři společnosti. Ten ale pracoval na podobném tématu a z žárlivosti rozběhl dost nechutný spor.
Roku 1851 Leon Foucault provedl pokus s koulí o hmotnosti 30 kg, kterou zavěsil na ocelovém drátě délky 67 m v kupoli pařížského Panteonu. Při kývání kyvadla docházelo ke stáčení roviny kyvu. Foucault tak dokázal rotaci Země. Podobné pokusy prováděl už o 200 let dříve Vincenzo Viviany, když opakoval pokusy Galilea Galileiho. Považoval je za anomálii způsobenou závěsem kyvadla.

Foucaultovo kyvadlo v pařížském Pantheonu.
Zdroj: commons.wikimedia.org. Autor: Javi Masa. Under Creative Commons.
Je více možností, jak realizovat Foucaultovo kyvadlo. Jednou z nich je kyvadlo s dlouhým, pevným lankem a těžkým závažím. Styl zavěšení nesmí bránit stáčení roviny kyvu (nebo ji naopak podporovat). Nepřípustné je například zavěšení do V. Foucaultovo kyvadlo musí mít především malé tlumení (tj. vydrží kývat dlouho), nejvhodnějším tvarem závaží je pro svou symetrii koule. Při nesymetrických tvarech dochází k nerovnoměrnému obtékání vzduchu, jehož důsledkem je vždy nějaká rušivá síla.
V důsledku rotace Země působí na každé pohybující se těleso tzv. Coriolisova síla. Jev stáčení kyvadla lze vysvětlit také tak, že kyvadlo ve skutečnosti rovinu kyvu zachovává, ale Země se pod ním otáčí. Foucaultovo kyvadlo tedy zachovává rovinu kyvu vzhledem ke stálicím (a s přijatelnou přesností lze říci, že vzhledem ke Slunci). Stáčení je pomalé, prostým okem v podstatě nepozorovatelné. Jednou z variant demonstrace je mít k dispozici kvalitní Foucaultovo kyvadlo, to rozkývat a nechat kývat dlouho (třeba několik hodin). Stáčení roviny kyvu je pak zřetelné. Na pólech činí toto stáčení 360° za 24 hodin (což odpovídá 15° za hodinu). V jiných zeměpisných šířkách se rovina kyvu stočí o úhel α za dobu t
![]()
Kde φ je zeměpisná šířka. V Praze je to přibližně 11,5° za hodinu, což je téměř 1° za pět minut. Na rovníku k jevu nedochází. Na severní polokouli se rovina kyvu stáčí po směru hodinových ručiček (pozorováno z místa závěsu), na jižní polokouli je tomu obráceně.
Druhým důkazem rotace Země je určení dopadu tělesa padajícího z určité výšky. Kdyby nebyla rotace, tak by volně padající těleso dopadlo přesně svisle dolů. Protože se ale Země otáčí, má výchozí místo větší úhlovou rychlost než místa, kterými těleso prochází při pádu a která jsou bližší středu Země. A protože těleso má stále větší úhlovou rychlost, musí předbíhat místo dopadu. První měření, která měla tento předpoklad potvrdit, provedl v Bologni v letech 1790 – 1792 Guglielmini a v roce 1903 je zopakoval Camille Flammarion v Paříži. Na dalším obrázku je reprodukce jeho náčrtu dopadových bodů z výšky 68 m. Většina dopadových bodů směřuje podle teoretického předpokladu na východ a černou tečkou je vyznačeno nejpravděpodobnější místo dopadu.
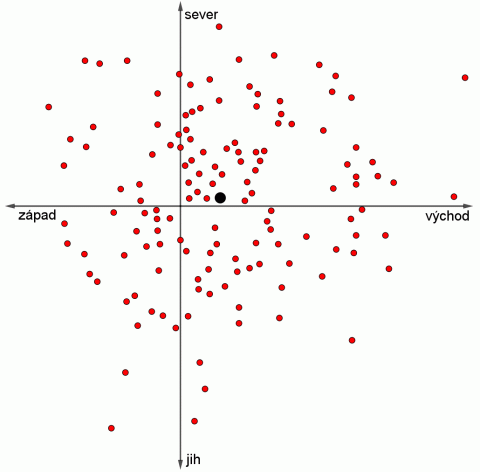
Měření místa dopadu Camilla Flammariona.
Zdroj: Nussbberger, J. Viditelné záření. Praha: Orbis, 1963. 2. vydání.
Všechny pohyby Země (kolem Slunce a kolem vlastní osy) se skládají. Proto od půlnoci do poledne se rychlost otáčení Země přičítá k postupné rychlosti Země, od poledne do půlnoci se odečítá. V prvním případě se proto pohybujeme se Zemí rychleji.
