Ze zkušenosti víte, že automobil s výkonnějším motorem, který vyvine větší tažnou sílu, se rozjíždí s větším zrychlením než automobil o stejné hmotnosti, jehož motor má menší tažnou sílu. Také víte, že chcete–li uvést auto do pohybu s větším zrychlením, musíte na něj působit větší silou. Větší síla působící na těleso je příčinou jeho pohybu s větším zrychlením.
Rovněž jste si mohli všimnout, že nákladní automobil s nákladem o větší hmotnosti se rozjíždí pomaleji, tj. s menším zrychlením, než tentýž automobil bez nákladu. Těleso s větší hmotností se působením určité síly pohybuje s menším zrychlením. Vztah mezi veličinami zrychlení, síla a hmotnost můžeme shrnout:
Mutationem motus proportionalem esse vi motrici impressae et sieri secundum lineam rectam qua vis illa imprimitur.
Změna množství pohybu je úměrná vnucené síle a probíhá podél přímky, u které tato síla působí.
Dnešní formulace zákona pochází od Leonharda Eulera:
Zrychlení tělesa je přímo úměrné síle F, která na těleso působí a nepřímo úměrné hmotnosti m tělesa, tedy
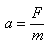
Dosazením jednotek získáme pro jednotku newton: kg m s-2.
Druhý Newtonův zákon můžeme upravit. Uvažujme automobil o hmotnosti m, jehož motor působí tažnou silou F. Tato tažná síla mu umožnila zrychlit z rychlosti v1 na rychlost v2. Pro změnu rychlosti tedy platí Δv = v2 – v1, a proto zrychlení ve vztahu můžeme nahradit
![]()
Celou rovnici vynásobíme časem Δt
![]()
dostaneme na levé straně rovnice součin FΔt, který představuje veličinu zvanou impuls síly, tedy
![]()
Jednotkou je newtonsekunda, značka N s. Součin mΔv na pravé straně představuje změnu hybnosti Δp.
Jestliže chceme změnit hybnost tělesa, musíme působit po určitou dobu silou. O velikosti změny hybnosti rozhoduje nejen síla, ale i doba, po kterou síla působí. Proto i malá síla, která působí po dlouhou dobu, může mít velké pohybové účinky. Pomocí změny hybnosti můžeme také přepsat druhý Newtonův zákon jako
![]()
Tento zápis druhého Newtonova zákona se nazývá první věta impulsová a říká, že časová změna celkové hybnosti tělesa je rovna součtu všech vnějších sil, které působí na těleso.
Řadu těchto veličin a vztahů si můžeme vysvětlit na příkladu sekyrky a sekání dřeva. Účinek sekyrky není jednoznačně dán tím, jakou silou zabereme za topůrko. Jakmile sekyrku zvedneme nad hlavu, působí při pohybu dolů ruce společně s gravitační silou. Účinek těchto sil – švunk – představuje hybnost sekyrky. Ta závisí nejen na rychlosti pohybu sekyrky, ale také na její hmotnosti. Čím je sekyrka těžší, tím větší hybnost a „švunk“ bude mít. Podle předchozího vztahu představuje změna hybnosti časovou změnu síly, proto i účinky sekyrky při sekání dřeva závisí na době působení, tzn. že čím rychleji sekyrkou švihneme, tím můžeme působit menší silou a účinky při štípání jsou stejné.
Použité zdroje:
[1] KUBĚNA, J. O Newtonových a Keplerových zákonech aneb, jak asi Newton na své zákony přišel. Matematika Fyzika Informatika: časopis pro výuku na základních a středních školách, duben 1998, roč. 7, č. 7-8, s. 409-416, 472-482. ISSN 1210-1761.
