Ohyb světla omezuje rozlišovací schopnost optických přístrojů. Jestliže pozorujeme dva vzdálené objekty s nepatrným zorným úhlem, např. dvě hvězdy, které jsou na obloze blízko u sebe. V důsledku Fraunhoferova ohybu zobrazí dalekohled každou hvězdu jako jasné kolečko obklopené soustřednými tmavými a světlými pruhy. Jestliže jsou oba objekty příliš blízko sebe, střední světlé části splynou a hvězdy není možno rozlišit.
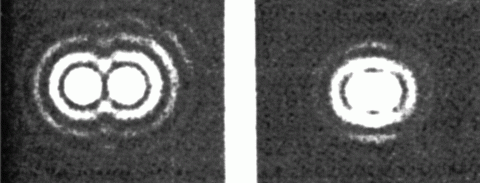
Ohyb světla hvězdy při pozorování dalekohledem.
Zdroj: commons.wikimedia.org. Under Creative Commons.
Základním kriteriem pro rozlišovací mez optických přístrojů je Rayleighovo kritérium: při zobrazování dvou bodů se obě stejně velké složky zobrazí jako dva různé objekty, jestliže je vzdálenost jejich středů rovna alespoň součtu jejich poloměrů.
Jestliže necháme procházet monochromatické světlo dvěma blízkými štěrbinami, tzv. dvojštěrbinou, dojde na každé štěrbině k ohybu světla. Vlnění získaná na jednotlivých štěrbinách jsou koherentní a na stínítku interferují. Zjednodušeně zachycuje situaci obrázek.
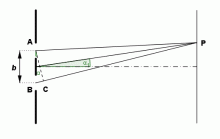
Vznik ohybového obrazce na dvojštěrbině.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.
Vzdálenost středů štěrbin označíme b, polohu bodu P na stínítku určíme úhlem α. Rozdíl délek úseček BP a AP reprezentuje optický dráhový rozdíl BC interferujících vlnění. Z pravoúhlého trojúhelníku ABC s ostrým úhlem α při vrcholu A lze tento rozdíl vyjádřit vztahem
![]()
V bodě P nastává pro světlo s vlnovou délkou λ interferenční maximum tehdy, je–li dráhový rozdíl roven celistvému násobku vlnové délky,
![]()
Interferenční minimum je v bodě P tehdy, je–li dráhový rozdíl roven lichému násobku poloviny vlnové délky, tedy
![]()
Při použití monochromatického světelného zdroje dostaneme na stínítku střídavé tmavé a světlé proužky v bodech, které odpovídají podmínkám maxima a minima pro různé hodnoty úhlu α. Pro α = 0° nastává nejintenzivnější maximum v bodě P0, které označujeme jako maximum nultého řádu bsin α = 0λ. V jistém bodě P1 je maximum prvního řádu bsin α = 1λ apod.
Z uvedeného vztahu plyne, že čím menší rozměry mají jednotlivé štěrbiny mřížky a čím blíže jsou k sobě, tím větší je rozteč jednotlivých maxim difrakčního obrazce. Velikost úhlu ohybu se bude zvyšovat s rostoucí vlnovou délkou (tzn. s klesající frekvencí) použitého světla. To se projeví na difrakčním obrazci – rozteč jednotlivých maxim se bude s rostoucí (resp. klesající) vlnovou délkou rozšiřovat (resp. zužovat). Z výše uvedeného vyplývá důležitá vlastnost difrakčních mřížek, a sice, že mají, podobně jako třeba hranol, schopnost disperze světla. K disperzi na mřížce ovšem dochází v opačném smyslu než u hranolu. Hranol totiž láme nejvíce světlo z fialového konce spektra a nejméně z červeného konce spektra, kdežto u difrakční mřížky je tomu přesně naopak (anomální disperze).
Nejvýraznější ohybové jevy pozorujeme pomocí tzv. optické mřížky, která slouží k periodickému ovlivnění fáze nebo amplitudy vstupujícího světla. Rozlišujeme mřížky transparentní (průhledné), reflexní (odrazové) a difrakční (ohybové). U difrakčních mřížek se pravidelně střídají propustné a nepropustné části mřížky (bílá/černá). U transparentních mřížek je výsledný efekt zajištěn buďto periodicky proměnou tloušťkou destičky, nebo periodickým střídáním indexu lomu u destičky s konstantní tloušťkou. Reflexní mřížky jsou potom založeny na odrazu světla. Vzdálenost středů štěrbin (v předchozích vztazích označená b) se nazývá mřížková konstanta. Průchodem světla mřížkou získáváme mřížkové spektrum. Vzniká interferencí koherentních vlnění získaných na každé štěrbině mřížky. Podle podmínky pro maxima lze snadno zdůvodnit, že v mřížkovém spektru se nejvíce odchyluje světlo červené.

Jemné vrypy o šířce 0,5 mm na kompaktním disku dělají z disku difrakční mřížku. Svítí-li na disk malý zdroj bílého světla, tvoří difraktované světlo barevné pruhy, které jsou směsicí difrakčních obrazců od vrypů.
Zdroj: commons.wikimedia.org. Under Creative Commons.
Jestliže použijeme k difrakci rentgenové záření, musíme i překážku zmenšit na rozměry vlnové délky rentgenového záření. Tomu odpovídají rozměry řádově 10–10 m, tedy rozměry v krystalické mřížce. Rentgenová difrakce nám tak poskytne důležité informace o vnitřní struktuře krystalů. Tento významný objev pochází z roku 1912 od Maxe von Lauea. Dalším výzkumem se zabývali William Henry Bragg a jeho syn William Lawrence Bragg. Rentgenová difrakce velmi pozitivně ovlivnila rozvoj celé přírodovědy, neboť jejím prostřednictvím byla nalezena struktura obrovského počtu látek (řádově 105) a teorie difrakce také umožnila zrod celých vědních disciplín (např. molekulární biologie). Jde vlastně o difrakci Fraunhoferova typu, neboť se měří difraktovaná intenzita v závislosti na směru. Avšak objekt, na němž k difrakci dochází, je trojrozměrný krystal, a ne rovinné difrakční stínítko jako v případě optické difrakce.
V roce 1953 Francis Crick a Jim Watson studovali rentgenový ohybový obrazec způsobený molekulou DNA, který pořídila Rosalinda Franklinová. Z jeho tvaru usoudili, že molekula DNA musí být uspořádána do dvojité šroubovice.

