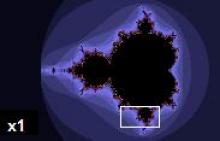
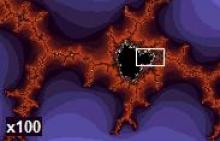
Fraktály objevil Benoît Mandelbrot v roce 1980, když experimentoval s matematikou. Že s ní experimentovat nejde? Ale ano, ale je k tomu potřeba počítač a tiskárna, i když v jeho případě velmi stařičká tiskárna Tektronix. Mandelbrot nechal počítač vypočítávat hodnoty výrazu z2 + c, kde z a c jsou komplexní čísla a c je konstanta. Hodnotu konstanty si zvolil, třeba c = 1 + i, hodnota z začíná od nuly. Pak dosadil z = z2 + c = 0 + 1 + i = 1 + i, tuto hodnotu dosadil znovu z = z2 + c = (1 + i)2 + 1 + i = 1 + 2i + i2 + 1 + i = 1 + 3i. A tak pořád dál a dál. Výsledné hodnoty znázornil do Gaussovy komplexní roviny a nestačil se divit.
Mandelbrotova množina.
Zdroj: commons.wikimedia.org. Autor: Wolfgang Beyer. Under Creative Commons.
Na papíře se mu objevil nádherný a zajímavý obraz dnes nazývané Mandelbrotovy množiny. Když si ho přiblížil, tak zjistil, že zase vidí ten stejný detail. Od Mandelbrota také pochází označení fraktálů. Mandelbrot se o svém objevu vyjádřil takto: „Tato množina je úžasnou kombinací vrcholné jednoduchosti a závratné komplikovanosti. Na první pohled se jedná o jednu „molekulu“ z vázaných „atomů“, z nichž jeden vypadá jako srdce a druhý je téměř kruhový. Podíváme-li se z větší blízkosti, objevíme nekonečné množství menších molekul, které jsou tvarovány přesně tak, jako velká molekula a navzájem jsou spojeny něčím, co nazýváme „ďábelským polymerem“.“
Zvětšení Mandelbrotovy množiny.
Autor: Nadim Ghaznavi. Under GNU Licence.
Podobně jak vzniká Mandelbrotova množina, tak vzniká i Juliova množina, kterou definoval Gaston Julia v komplexní rovině. Mandelbrot měl své předchůdce již o sto let dříve. Ti bohužel neměli počítače, které by jejich myšlenky dotáhly dál a ukázaly jejich grafickou podobu. Prvním předchůdcem Mandelbrota byl Georg Cantor a jeho diskontinuum publikované v roce 1883. Cantorovo diskontinuum vzniká dělením libovolné úsečky na třetiny, z níž se v dalším kroku prostřední třetina vyloučí. Tak se pokračuje dál a dál.
Cantorovo diskontinuum.
Zdroj: commons.wikimedia.org. Public domain.
První fraktální křivkou je Kochova vločka od Nielse von Kocha z roku 1904. Von Koch vycházel z rovnostranného trojúhelníku, jehož strany rozdělil na třetiny, nad prostřední sestrojil nový rovnostranný trojúhelník a jeho základnu vymazal. Takto postupoval u dalších tří trojúhelníků. Kochova křivka zůstává stále uvnitř kruhu, má tedy konečnou plochu, ale nekonečný obvod. Obsah Kochovy vločky je 8/5 původního rovnostranného trojúhelníku.
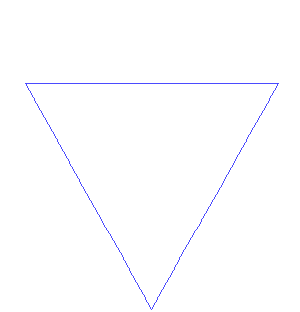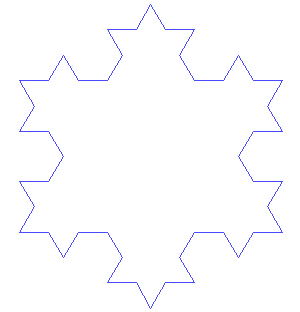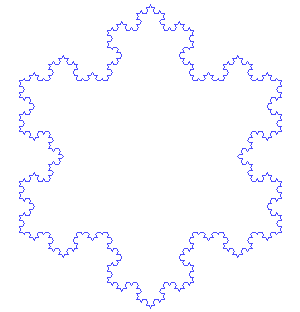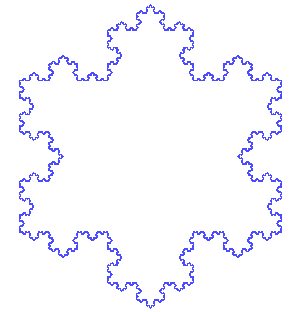
Vznik von Kochovy vločky a Kochova antivločka.
Zdroj: commons.wikimedia.org. Autor: António Miguel de Campos (Kochova vločka). Public domain. Under Creative Commons.
Kochova vločka má řadu modifikací, třeba Kochova antivločka, která vzniká tak, že trojúhelníky při každém kroku směřují dovnitř původního trojúhelníku.
Dalším slavným fraktálem je Sierpińského trojúhelník z roku 1916 od Wacława Sierpińského, který vzniká postupným odečítáním rovnostranných trojúhelníků od základního rovnostranného trojúhelníku. Podobu Sierpińského trojúhelníku má i Pascalův trojúhelník, jestliže v něm vybarvíme všechna prvočísla.
Vznik Sierpińského trojúhelníku.
Zdroj: commons.wikimedia.org. Public domain.
Modifikací Sierpińského trojúhelníku je Sierpińského koberec, který vznikne stejným způsobem, ale výchozím objektem je čtverec. Do prostoru modifikoval Sierpińského koberec Karl Menger a útvar nese označení Mengerova houba.
Mengerova houba.
Zdroj: commons.wikimedia.org. Under Creative Commons.
Podobných geometrických fraktálů je mnoho. Stačí vzít výchozí objekt a neustále na něj aplikovat vybraný postup.
A dají se tyto krásné geometrické obrazce někde použít? Odpověď najdeme v Mandelbrotově aforismu: „Mraky nejsou kulovité, kopce nejsou kuželovité, kontury pobřeží netvoří kruhy a kůra není hladká, také blesk se nepohybuje po přímce.“ V každém slově této věty Mandelbrot vyjádřil nedostatečnost eukleidovské geometrie při popisu reálného světa a zároveň potenciál fraktálů.
Fraktály jsou stále otevřeným problémem. Nacházejí uplatnění při modelování růstu rostlin, růžiček květáků, v meteorologii při modelování vzniku a vývoje oblačnosti, v medicíně při modelování mozkové aktivity.
Použité zdroje:
[1] CRILLY, T. Matematika. 50 myšlenek, které musíte znát. 1. vydání. Praha: Slovart, 2010. ISBN: 978-80-7391-409-7.
[2] DIVIŠOVÁ, B. Fraktály a jak o nich učit. Učitel matematiky, březen 2013, roč. 21, č. 3 (87), s. 144–158. ISSN 1210–9037.
