O konstrukci pravidelného sedmiúhelníku se pokoušel už Archimedes. Po dlouhou dobu byly snahy matematiků marné. Vypadalo to, že pravítkem a kružítkem tento pravidelný obrazec sestrojit nepůjde. Byly nalezeny přibližné metody, např. z konstrukce pravidelného pětiúhelníku je to přibližně úsečka FH. Tuto otázku uzavřel až Carl Gauss v roce 1801 tím, že zjistil, které pravidelné mnohoúhelníky je možné sestrojit pravítkem a kružítkem. Podle jeho důkazu lze sestrojit pravidelný n-úhelník pravítkem a kružítkem tehdy, když je n číslo ve tvaru
![]()
Kde s je celé číslo kladné nebo nula a p1, p2, … pk jsou Fermatova prvočísla. Ta splňují podmínku, že jsou ve tvaru 2m + 1, kde m jsou prvočísla a 0. Jediná známá jsou Fermatova prvočísla jsou 3, 5, 17, 257 nebo 65 537. Formulace zní složitě. Pojďme si ukázat, které to jsou n-úhelníky. Hodnoty n pak mohou být 3 (s = 0, m = 1), 4 (s = 2, m = 0), 5 (s = 0, m = 2), 6 (s = 1, m = 1), 8 (s = 3, m = 0), 10 (s = 1, m = 2), 12 (s = 2, m = 1), 15 (s = 0, m = 1, 2), 16 (s = 4, m = 0), 17 (s = 0, m = 4). Konstrukci pravidelného 17ti úhelníku nalezl Gauss už v devatenácti letech. Gaussova konstrukce vychází ze dvou vlastností čísla 17: je to prvočíslo a zároveň je o jedničku větší než druhá mocnina čtyř. Gauss konstrukci dokázal algebraicky a dál se jí nezabýval.
Postup konstrukce pravidelného pětiúhelníku vepsaného kružnici s poloměrem r a středem A
- Sestrojíme libovolný průměr kružnice CD
- Sestrojíme pomocnou kružnici se středem v bodě C a poloměrem r
- Obě kružnice se protnou v bodech E, F; úsečka EF je osou úsečky CA
- Bod H je průsečík osy a úsečky CA
- Sestrojíme kružnici se středem H, která prochází bodem B (koncový bod průměru kolmého na CD)
- Průnik této kružnice a přímky CD je bod L
- Vzdálenost BL je hledaná strana pravidelného pětiúhelníku
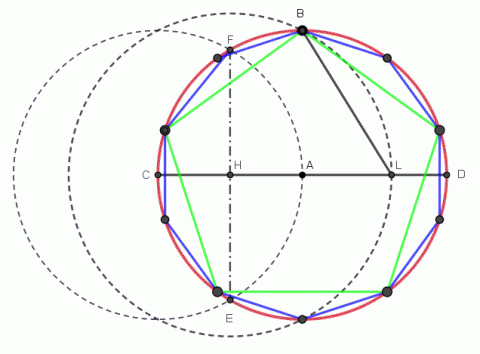
Konstrukce pravidelného pětiúhelníku.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.
Vzdálenost CD odpovídá straně pravidelného trojúhelníku, vzdálenost CB odpovídá straně pravidelného čtyřúhelníku, vzdálenost AB odpovídá straně pravidelného šestiúhelníku, vzdálenost AL odpovídá straně pravidelného desetiúhelníku.
Použité zdroje:
[1] BEUTELSPACHER, A. Matematika do vesty. Praha: Baronet, 2005. ISBN 80-7214-841-9.
[2] SEDLÁČEK, J. Nebojte se matematiky. Praha: SNTL, 1960.
[3] STEWART, I. Kabinet matematických kuriozit profesora Stewarta. Praha: Dokořán, 2013. ISBN 978-80-7363-292-2.
