Teselace

Pokud se snažíme rovinu zaplnit beze zbytku rovinnými obrazci, pak hovoříme o tzv. teselaci nebo mozaice, dlažbě. Teselace nejsou zajímavé jen pro designéry jako vzory na tapety, látky nebo dlažby, ale používají se třeba i k popisu uhlíkatých nanotrubic a objevují se v přírodě jako krystalové a buněčné struktury.

Pokud bychom chtěli rovinu překrýt jen jedním druhem pravidelného rovinného obrazce, pak se nám to podaří se čtvercem, rovnostranným trojúhelníkem a pravidelným šestiúhelníkem. Takové teselace byly dobře známé Johannesu Keplerovi, který o nich psal v Harmonices Mundi a byl pravděpodobně prvním, kdo se jimi zabýval z pohledu matematiky.

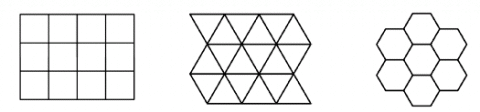
Pokrytí roviny čtverci, pravidelnými trojúhelníky a pravidelnými šestiúhelníky.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.

Otázkou je, zda je takových pravidelných n-úhelníků, které pokryjí rovinu, více. Pro vnitřní úhel pravidelného n-úhelníku platí

Aby byla rovina zcela pokryta, je nutné, aby 360° (plný úhel) byl dělitelný velikostí vnitřního úhlu pravidelného n-úhelníku. Musí tedy platit, že podíl

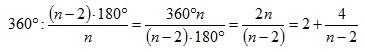
Při dosazení n = 3, n = 4 a n = 6 to platí. Pro jiná čísla ne.

Rovinu také můžeme pokrýt nepravidelnými n-úhelníky. Podaří se nám to s libovolným trojúhelníkem a čtyřúhelníkem (i nekonvexním), některými konvexními pětiúhelníky a šestiúhelníky a nikdy se nám rovinu nepodaří pokrýt s n-úhelníků, kde n je větší nebo rovno sedmi.

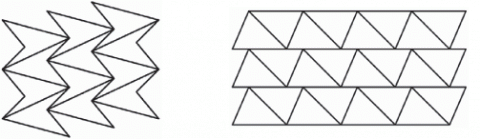
Pokrytí roviny nekonvexním čtyřúhelníkem a nepravidelným trojúhelníkem.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.

Objev, které konvexní šestiúhelníky vytvářejí teselaci, je připisován Karlu Reinhardtovi, který ve své dizertační práci z roku 1918 našel řešení tohoto problému. Rovinné teselace vytvářejí právě tři typy konvexních šestiúhelníků. (Typem se rozumí takový šestiúhelník, který vyhovuje podmínkám pro velikost stran a vnitřních úhlů.) Podobně stanovil Reinhardt pět typů pětiúhelníků vytvářejících rovinné teselace. Dlouho se považovala tato klasifikace za uzavřenou. Až v roce 1968 doplnil Richard Kershner počet pětiúhelníkových teselací o další tři typy, Martin Gardner v roce 1975 o jednu, Marjorie Rice o čtyři, Rolf Stein o jednu a poslední pochází z roku 2005 a na jejím objevu se podíleli Casey Man, Jennifer McLoud a David Von Derau. Celkem je tedy 15 pětiúhelníkových teselací.

Patnáct pětiúhelníkových teselací.
Zdroj: commons.wikimedia.org. Under Creative Commons.

Pokud budeme chtít pokrýt rovinu dvěma a více druhy pravidelných mnohoúhelníků s podmínkou, že se v každém bodu setkávají tři obrazce s vnitřními úhly α, β, γ s počtem stran x, y a z.

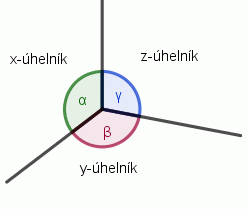
K odvození existujících teselací.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.

Pro úhly α, β, γ pak platí

Součet všech úhlů při úplném pokrytí roviny je 360°, proto pro úhly α, β, γ musí platit

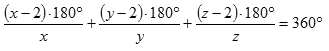
A po úpravě

Pokud tedy chceme určit jaké pravidelné útvary pokryjí rovinu, pak stačí najít tři čísla x, y, z, která jsou řešením této neúplné (diofantické) rovnice. Byla nalezena tato řešení

Řešení této rovnice je sice podmínka nutná, ne však dostačující. Vezměmě si hned první trojici x = 3, y = 7, z = 42 a podívejme se na následující obrázek

K odvození existujících teselací.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.

Pokud si nakreslíme trojúhelník, pak v bodě A se potkávají pravidelný sedmiúhelník, trojúhelník a 42-úhelník. V bodě B také, ale v bodě C nikoli. Tam se potkávají pravidelný trojúhelník a dva sedmiúhelníky. To je ale špatně. Proto můžeme tuto a podobné varianty vyškrtnou. Zůstává varianta 3, 12, 12; 4, 6, 12; 4, 8, 8 a 6, 6, 6, které jsou na obrázku.

 
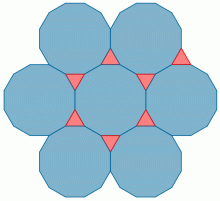
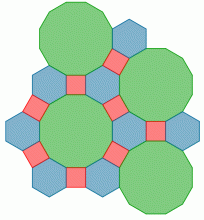
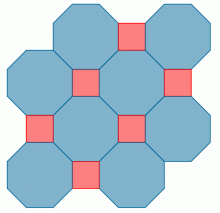
Teselace tvoření dvěma nebo třemi pravidelnými n-úhelníky.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.

Kromě periodických teselací existují i teselace neperiodické a aperiodické. Zastavme se u aperiodických. To jsou takové, v nichž se opakuje konečný počet tvarů dlaždic, ale nenalezneme žádnou opakující se část. První pokusy o nalezení aperiodické sady dlaždic pochází z roku 1966 od Roberta Bergera, který použil sadu dlaždic Hao Wanga. Tyto dlaždice jsou čtvercové a mohou mít buď obarvené hrany, nebo čtyři různobarevné pravoúhlé trojúhelníky, které vzniknou díky uhlopříčkám. Při sestavování mozaiky se pak přikládají k sobě hrany se stejnou barvou.

Příklad Wangovy sady dlaždic a Wangova teselace.
Zdroj: commons.wikimedia.org. Autor: Claudio Rocchini. Under Creative Commons.

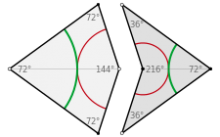
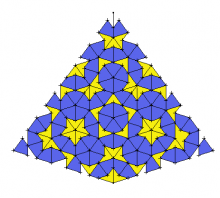
V roce 1974 Roger Penrose vytvořil tři sady dlaždic, ze kterých lze za určitých podmínek sestavit aperiodickou teselaci. První sada obsahuje šest dlaždic. Druhá sada obsahuje dvě dlaždice ve tvaru čtyřúhelníku, jedna ve tvaru draka a druhá ve tvaru šipky. Obě dohromady se dají složit do rovnoběžníku s vrcholovými úhly 72° a 108°.

Druhá Penroseova teselace.
Zdroj: commons.wikimedia.org. Under Creative Commons.

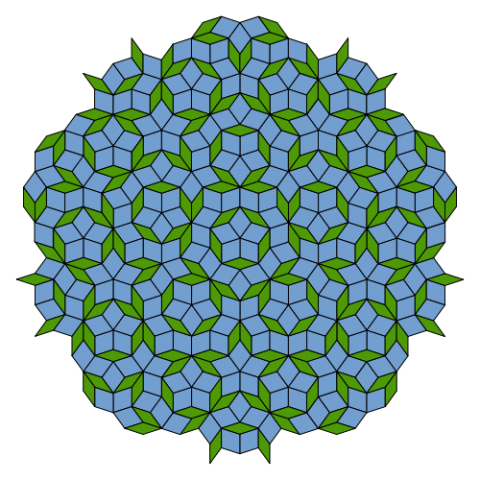
Třetí Penroseovu teselaci tvoří dva kosočtverce, jejichž úhly jsou 36° a 144° u jednoho a 72° a 108° u druhého. Kosočtverce se sestavují v mozaiku podle určitých pravidel. Podíl počtu větších a menších kosočtverců je v nekonečné Penrosově teselaci roven přesně zlatému řezu. Toto číslo je iracionální, a proto v Penrosově mozaice nelze definovat jedinou elementární buňku.

Penroseova teselace.
Zdroj: commons.wikimedia.org. Under Creative Commons.

Použité zdroje:

[1] ILUCOVÁ, L. História pentagonálních teselácií. In J. Bečvář, M. Bečvářová (eds.): Sborník sylabů 30. mezinárodní konference historie matematiky, Jevíčko 21. – 25. 8. 2009. Matfyzpress, Praha 2009, 128–133.

[2] SEDLÁČEK, J. Nebojte se matematiky. Praha: SNTL, 1960. 

[3] ŠVECOVÁ, R. Matematické základy tvorby ornamentálních tvarů. Diplomová práce. Plzeň, 2010.