Stavidlo na Pstružném potoce.
Zdroj: commons.wikimedia.org. Public domain.
Teorie
Pro technickou praxi má velký význam studium tekutin v pohybu. Převažuje–li pohyb tekutiny v jednom směru, pak hovoříme o proudění. Tekutina mezi dvěma místy proudí tehdy, jestliže je mezi nimi rozdíl tlaků. Trajektorie jednotlivých částic proudící tekutiny znázorňujeme proudnicemi. Tečna sestrojená v určitém bodě k proudnici určuje směr rychlosti pohybující se částice tekutiny v tomto bodě. Kolem aerodynamických těles probíhá laminární proudění – proudění bez vírů. Při turbulentním proudění se za tělesem tvoří víry. Tlak za tělesem je menší než před tělesem a to způsobí růst odporové síly. Turbulentní proudění vody se projevuje např. šumem vody ve vodovodním potrubí.
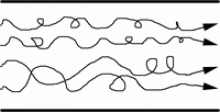
Laminární a turbulentní proudění.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.
Nejjednodušším příkladem laminárního proudění je ustálené proudění ideální kapaliny, které je charakterizováno stálou rychlostí a stálým tlakem kapaliny v určitém libovolně zvoleném místě toku. Při ustáleném proudění protéká každým průřezem potrubí za stejnou dobu stejný objem kapaliny, takže kapalina se v žádném místě nehromadí.
Uvažujme ustálené proudění ideální kapaliny vodorovnou trubicí. Protéká–li průřezem S částice kapaliny rychlostí v, proteče jím za jednu sekundu kapalina o objemu V. Objem kapaliny, který proteče daným průřezem trubice za jednotku času, se nazývá objemový průtok a značí se QV a vypočítá jako
Je–li v rychlost proudící kapaliny, posune se za dobu t každá částice kapaliny průřezem trubice o dráhu s = vt. Označíme–li obsah průřezu S, je objem kapaliny V = Svt. Po dosazení dostaneme pro objemový tok
Objemový průtok měříme v jednotkách m3/s. Objem vody, která proteče daným potrubím za libovolnou dobu, měříme vodoměrem, objem plynu plynoměrem. Skládá se z lopatkového kola, jehož pohyb se převádí ozubenými převody na počitadlo.
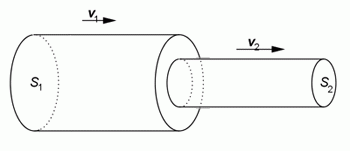
Potrubí s různým průřezem.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.
Poněvadž objemový průtok je v libovolném průřezu trubice stejný, pohybují se částice kapaliny v zúženém místě trubice větší rychlostí. Je–li v průřezu S1 rychlost proudu kapaliny v1, proteče jím za 1 s objem stejný jako v průřezu S2, kde je rychlost proudu v2. Tedy
Při ustáleném proudění ideální kapaliny je součin obsahu průřezu potrubí a rychlosti proudu pro všechny průřezy stálý. Uvedený vztah se nazývá rovnice spojitosti nebo rovnice kontinuity. Z rovnice spojitosti vyplývá, že rychlost proudu kapaliny je nepřímo úměrná průřezu trubice. Proto kapalina protéká menším průřezem větší rychlostí než velkým. Vzhledem k tomu, že rovnice spojitosti platí přesně jen pro ideální kapalinu, je rychlost skutečné kapaliny, mezi jejímiž částicemi působí síly vnitřního tření, menší.
Při proudění tekutiny dochází ke strhávání drobných předmětů, např. písku nebo kamínků na dně koryta. Zákonu strhávání se říká Airyho zákon a říká, že n–násobně rychlejší proud je schopen strhávat n6krát těžší předměty. I když tento zákon zní podivně, ukážeme si jeho platnost na příkladu tří řek, jejichž rychlosti jsou v poměru 1:2:4. Podle Airyho zákona bude poměr vah kamenů unášených proudy řek 1:64:4096, tzn. že klidná řeka sotva unáší pískové zrníčko o hmotnosti 0,25 g, dvakrát rychlejší řeka už unese kamínky o hmotnosti 16 g a ještě dvakrát prudší horská říčka je schopna strhávat kameny o váze jednoho kg.
Hydrostatický tlak ve stejné hloubce kapaliny je stejný. To však platí jen pro kapaliny v klidu. Jak je tomu u proudící kapaliny? U proudící kapaliny v potrubí, které má různé průměry, není tlak ve všech místech stejný. V místě s větším průřezem má proudící kapalina větší tlak, ale menší rychlost, zatímco v místě s menším obsahem průřezu má menší tlak, ale větší rychlost. Protože v proudící kapalině se nemůže měnit mechanická energie v jiné formy energie, je součet kinetické a tlakové potenciální energie v jednotkovém objemu kapaliny pro oba průřezy trubice stejný. Platí tedy
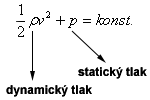
Tento vztah se nazývá Bernoulliho rovnice a poprvé ji formuloval Daniel Bernoulli. Vyjadřuje zákon zachování energie ideální kapaliny proudící ve vodorovné trubici. Platí i pro plyny. Ty ale při malé změně teploty mění své fyzikální vlastnosti – hustotu, viskozitu apod. a navíc na rozdíl od kapalin jsou stlačitelné.
Daniel Bernoulli.
Zdroj: Techmania Science Center. Autor: Pavel Trnka. Under Creative Commons.
Základní tvar Bernoulliho rovnice platí jen pro ideální kapaliny, kde je průtok beze ztrát. Pro reálnou kapalinu se Bernoulliho rovnice doplňuje o ztrátovou výšku. Ke ztrátám dochází díky tření o stěny nádoby díky náhlé změně směru proudící kapaliny.
Z Bernoulliho rovnice vyplývá, že tlak proudící kapaliny klesá s rostoucí rychlostí. Při velkém zúžení trubice, kde rychlost proudu kapaliny značně vzroste, může tlak v kapalině klesnout tak, že bude menší než tlak atmosférický – v zúženém místě trubice vzniká podtlak. Jestliže v této zúžené části bude otvor, pak bude z okolí nasávat vzduch. Tento jev se také nazývá hydrodynamické paradoxon. Podtlak u proudícího vzduchu se využívá např. u rozprašovače, stříkací pistole, karburátoru nebo vodní vývěvy.
Ze zákona zachování energie v proudící kapalině určíme rychlost kapaliny vytékající otvorem v nádobě. Jestliže nad otvorem je výška hladiny h, pak pro rychlost výtoku kapaliny platí Torricelliho vzorec
Čím více kapaliny vyteče, tím menší sloupec kapaliny bude nad otvorem, a proto bude i menší rychlost, kterou kapalina vytéká. U reálných kapalin je díky tření výtoková rychlost i množství vyteklé kapaliny menší. Proud kapaliny nevyplňuje úplně výtokový otvor, neboť proudnice se nemohou náhle přizpůsobit změně průřezu. Množství vytékající kapaliny může klesnou až na 62 % teoretické hodnoty.
