Záření černého tělesa

Koncem 19. století se zdálo, že fyzika dosáhla vrcholu svého vývoje. Objevily se však nesrovnalosti, které se zpočátku považovaly za maličkosti, ale postupně se na nich vybudovaly nové teorie. Jednou z těchto maličkostí byly odchylky experimentálních výsledků od teorie záření černého tělesa. Abychom lépe mohli studovat zákonitosti záření těles, zavedeme fyzikální abstrakci, tzv. černé těleso. Černé těleso dokonale pohlcuje veškerou energii, která na těleso dopadá. Nedochází k žádnému odrazu záření, takže za nízké teploty se nám jeví dokonale černé. Vlastnostem černého tělesa se nejvíce blíží dutina, jejíž vnitřní povrch tvoří matná černá plocha. Když otvorem v dutině pronikne dovnitř elektromagnetické záření, tak se při opakovaných odrazech od stěn dutiny veškerá energie záření pohltí. Otvor dutiny se pak jeví jako černý. Příkladem černého tělesa je i zornice, která se nám jeví jako úplně černá, ačkoli optické prostředí za ní (čočka a sklivec) je dokonale průhledné. Světlo, které vstupuje zornicí do oka, se uvnitř téměř všechno pohltí. Z oka pak nevystupuje žádné odražené záření a jeho vstupní otvor se nám jeví černý. Ze stejného důvodu jsou černá nebo alespoň tmavá při pohledu z ulice také okna bez záclon.

Rozhodující experimenty se zahřátým černým tělesem provedli v roce 1895 Otto Lummer a Ernst Pringsheim. Podle Gustava Roberta Kirchhoffa je množství energie, kterou vyzáří určitá plocha černého tělesa, závislé na jeho teplotě. Proto Lummer a Pringsheim použili kovovou skříňku zahřátou na teplotu T, ze které vycházelo otvorem záření. To se skleněným hranolem rozkládalo a na detektoru se měřila energie dopadajícího záření pro jednotlivé vlnové délky.

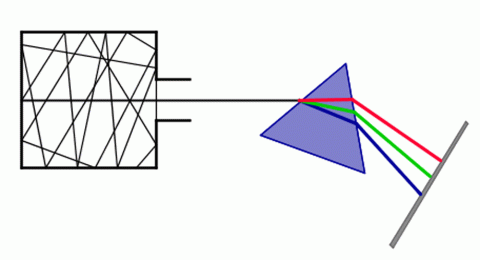
Znázornění experimentu Lummera a Prigsheima.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.

Pro jednotlivé teploty T pak vynesli graf v závislosti na vyzářené vlnové délce.

Graf závislosti spektrální hustoty vyzařování na vlnové délce.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.

M_λ je spektrální hustota vyzařování a určuje, jaká část celkové energie vyzářené zdrojem přísluší záření o vlnové délce λ při teplotě zdroje záření T. Graf na obrázku ukazuje, že při vyšší teplotě je celková vyzářená energie větší (zvětšuje se plocha vymezená grafem funkce) a největší hodnota M_λ se posouvá ke kratším vlnovým délkám. Vlnová délka λ_max odpovídá záření, které je při dané teplotě tělesem vyzařováno s největší intenzitou. Tím je vysvětleno, proč při nižší teplotě (přibližně 600 °C) se nám zahřáté těleso jeví jako červené. Při dalším zahřívání (přibližně 1 300 °C) se jeho barva mění na bílou, poněvadž jsou v záření zastoupeny všechny vlnové délky viditelné části spektra a ty se skládají. Při ještě vyšších teplotách se barva tělesa mění v modrobílou a těleso vyzařuje i ultrafialové záření (např. elektrody při obloukovém svařování). Tento jev můžeme využít u optické pyrometrie, metody na měření teplot nad 500 °C. Následující tabulka udává barvy pro jednotlivé teploty:

Teoreticky se jako první pokusil problém záření černého tělesa popsat Josef Stefan v roce 1879 a dospěl k výsledku, že vyzářená energie dutiny je úměrná čtvrté mocnině teploty.

kde σ = 5,6704 · 10^–8 W m^–2 K^–2 je Stefan–Boltzmannova konstanta. Stefanův zákon neřeší problém černého tělesa úplně. O to se pokusil v roce 1896 Wilhelm Wien, který tvrdil, že se největší zářivost černého tělesa při vzrůstající teplotě posouvá ve spektru ke kratším vlnovým délkám. Potvrzuje to spojnice vrcholů křivek. Závislost se nazývá Wienův posunovací zákon

kde b = 2,9 · 10^–3 m K. Na základě těchto poznatků můžeme odhadnout teplotu slunečního povrchu: Slunce s největší intenzitou vyzařuje žlutozelené světlo a tomu odpovídá teplota 5770 °C. Pro intenzitu vyzařování absolutně černého tělesa Wien odvodil

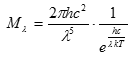
kde h je Planckova konstanta, c rychlost světla ve vakuu a k Boltzmanova konstanta. Wien pro teoretické vysvětlení záření černého tělesa použil analogii mezi fotony a molekulami plynu. Jeho teorie a výsledky pokusů Lummera a Prigsheima se plně shodovaly jen pro záření o malých vlnových délkách, pro dlouhovlnné záření zjistili systematické odchylky. Lord Rayleigh a ames Jeans zvolili pro odvození vyzařovacího zákona jinou cestu – statistickou fyziku. Jejich vzorec naopak plně popisoval záření dlouhovlnné a u krátkovlnného záření dával nesmyslné výsledky.

Např. při libovolné teplotě by podle jejich výpočtů měla být intenzita rentgenového záření velká, zdroj by měl vyzařovat nekonečně mnoho energie. Jde tedy o nesmysl, který do historie fyziky vešel pod názvem ultrafialová katastrofa. Tak byly odvozeny dva různé zákony pro spektrální zářivost, z nichž každý vyhovoval jen v určitém oboru vlnových délek. Wienův pro oblast ultrafialových vln, Rayleigh-Jeansův pro oblast infračerveného záření. V oblasti vln středních pak neplatil žádný. V roce 1900 Max Planck oba zákony zkombinoval. Předpokládal, že celkovou vyzářenou energii lze rozdělit na jednotlivé oscilátory. Energie každého oscilátoru je celočíselným násobkem nějaké nejmenší porce energie.

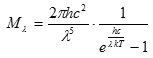
Planckův výsledek, vyvolaný zoufalým krokem, odpovídal experimentálním výsledkům skvěle. Zákony Wienův a Rayleighů–Jeansův dostaneme jako přibližné vztahy z Planckova vztahu. Pro malé λT je e^hc/λkT >>1 a tudíž 1 ve jmenovateli můžeme zanedbat a dostaneme Wienův zákon. Pro velké λT lze exponencielu ve jmenovateli nahradit přibližným vztahem (první dva členy Taylorova rozvoje e^x = 1+x) dostaneme Rayleigh–Jeansův zákon.

Planck situaci dál rozebral a zjistil, že není možné dál uvažovat nekonečně malá množství energie. Přeměna energie mechanické na zářivou nebo naopak není spojitá, ale děje se po celistvých násobcích určitého kvanta energie, nyní označované jako Planckova konstanta h = 6,625 · 10^–34 J s. Energie každé částice je jen po určitých porcích, tzv. kvantech (z lat. quantum – množství). Velikost této porce je úměrná frekvenci světla f a konstanta úměrnosti je jednou z fundamentálních fyzikálních konstant – Planckova konstanta h.