Bohrova teorie atomu nedokáže vysvětlit spektra atomů, které mají dva a více elektronů; nedokáže vysvětlit, proč jsou některé čáry intenzivnější než jiné; nemůže vysvětlit, proč se některé čáry skládají z několika jednotlivých čar, jejichž vlnové délky se jen nepatrně liší; a nedokáže vysvětlit vzájemnou interakci atomů.
Niels Bohr v roce 1920 přednášel na prestižní Göttingenské univerzitě. Tehdy za ním přišli dva mladí studenti, Wolfgang Pauli a Werner Heisenberg a upozornili ho, že hypotézu o jeho hýčkaných eliptických trajektoriích elektronů (které nikdo nikdy nepozoroval) fyzika nepotřebuje, že tyto trajektorie vlastně neexistují! Jediné, co lze pozorovat jsou frekvence a intenzity vyzařovaných spektrálních čar, což jsou jakési soubory čísel, z nichž lze vytvořit matematické objekty zvané matice a novou, maticovou podobu kvantové mechaniky. Bohr argumenty mladých studentů uznal a na dalším rozvíjení kvantové mechaniky, ať už maticové nebo vlnové, se podílel. Na základě matic, případně vlnové funkce, si ovšem atom nelze dost dobře představit, natož ho namalovat. Proto si stále atom zobrazujeme jako soubor eliptických orbit, v jejichž ohnisku je jádro.
Veličina, která charakterizuje de Broglieho vlny – vlny příslušející částicím, se nazývá vlnová funkce a označuje se Ψ. Hodnota vlnové funkce, příslušející pohybujícímu se tělesu v daném bodě o souřadnicích x, y, z prostoru a v čase t, souvisí s pravděpodobností výskytu tělesa v tomto bodě a čase. Vlnová funkce nemá sama o sobě žádný fyzikální význam. Je to proto, že pravděpodobnost, že těleso bude někde v daném čase, může nabývat libovolné hodnoty mezi 0 a 1. Ale amplituda každé vlny může být kladná i záporná, ale záporná pravděpodobnost nemá smysl. Proto vlnová funkce Ψ nemůže být pozorovatelnou veličinou. To se netýká | Ψ|2, kterou v roce 1926 navrhl Max Born použít jako hustotu pravděpodobnosti.
Protože amplituda de Broglieho vlny má charakter pravděpodobnosti výskytu částice v daném místě, nedá se de Broglieho vlna vyjádřit jednoduchou rovnicí jako je tomu např. u postupného vlnění. Místo toho je daleko zřetelnější prezentovat de Broglieho vlnu jako vlnové klubko, u kterého se amplituda mění s pravděpodobností výskytu.
De Broglieho vlnové klubko spojené s pohybujícím se tělesem se pohybuje se stejnou rychlostí jako těleso. Jeho poloha může být kdekoli uvnitř vlnového klubka. Jestliže je vlnové klubko velmi úzké, pak se velmi snadno určí jeho poloha, ale velmi nesnadno jeho vlnová délka. Jestliže je vlnové klubko velmi široké, pak se velmi snadno určí jeho vlnová délka, ale velmi nesnadno jeho poloha. Na základě této úvahy můžeme najít vztah mezi neurčitostí Δx měření polohy částice a neurčitostí Δp současného měření její hybnosti.
![]()
Tento vztah představuje princip neurčitosti (relaci neurčitosti), který poprvé získal Werner Heisenberg v roce 1927. Podle tohoto principu nemůžeme současně měřit polohu a hybnost s naprostou přesností. Experiment pak můžeme zařídit buď tak, že Δx je malé (úzké vlnové klubko) nebo že Δx je velké (široké vlnové klubko). Tyto neurčitosti nejde nijak přístrojově odstranit, představují přírodní zákon. Protože Planckova konstanta h v Heisenbergově principu neurčitosti je velmi malá (6,63 · 10–34 J s), týká se tento princip jen těles s atomovými rozměry.
Ve většině případů je velmi problematické určit vlnovou funkci Ψ. Vlnové funkce jsou řešením tzv. Schrödingerovy rovnice – základní rovnice vlnové mechaniky, kterou v roce 1926 formuloval Erwin Schrödinger. Schrödinger se domníval, že by funkci Ψ mohlo jít spojit s určitým typem kmitů v atomu, jejichž existence se mu zdála pravděpodobnější než Bohrem navržené trajektorie elektronů. Při kvantových přechodech spojených s vyzářením nebo pohlcením kvanta elektromagnetického záření, by tak energie pouze přecházela z jedné formy kmitů na jinou. Za jeden z nejpodstatnějších výsledků svého postupu považoval Schrödinger fakt, že jeho kvantovací pravidla neobsahovala požadavek celočíselnosti. Celočíselnost zde vyplynula jako důsledek obecných požadavků na funkci. Když se postupně ukázalo, že kvantových skoků se tak docela zbavit nelze, Schrödinger byl zjevně zklamaný. Traduje se, že v jednom z rozhovorů s Bohrem řekl: “Jestliže budeme muset jít dál s těmi prokletými kvantovými skoky, pak lituji, že jsem se do toho kdy míchal“. Bohr prý odpověděl: “Ale my ostatní jsme vám za to velmi vděčni, protože vaše práce udělala pro zdokonalení této teorie mnoho."
Pokusy ukázaly, že pravděpodobnost výskytu elektronu v obalu atomu má různou hodnotu v různých místech v okolí atomového jádra a mění se spojitě. Pro určitý kvantový stav elektronu má charakteristický prostorový tvar. Na obrázku je pro ilustraci v rovinném řezu znázorněno rozdělení pravděpodobnosti výskytu elektronu p na vzdálenosti od jádra r pro nejnižší energetický stav elektronu v atomu vodíku, a to jednak grafem a jednak hustotou tečkování (pravděpodobnost je kulově symetrická). Schrödingerův model lépe souhlasí s výsledky experimentů.
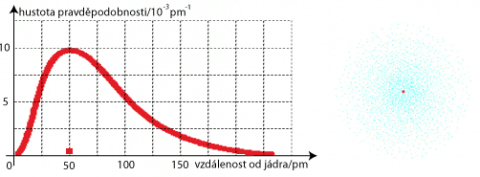
Závislost hustoty pravděpodobnosti na vzdálenosti od jádra. Obdélníková značka je umístěna ve vzdálenosti Bohrova poloměru atomu, tedy v místě s největší hustotou pravděpodobnosti výskytu elektronu. Obrázek vpravo představuje myšlenkový model atomu vodíku v základním stavu.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.
Atom můžeme považovat za rozmazanou kouli bez ostře definované hranice nebo přesně znázorněných orbitalů. Hodnoty energie, pro něž lze řešit Schrödingerovu rovnici se nazývají vlastní hodnoty a vlnové funkce, příslušné těmto hodnotám se nazývají vlastní funkce. Příkladem mohou být energetické hladiny vodíkového atomu odvozené Bohrem.
V roce 1926 přišel Erwin Schrödinger s vlnovou teorií v sérii článků nazvaných Quantisierung als Eigenwertproblem – představil částice jako prostorově ohraničené balíčky vln a snažil se tak získat názornou konstrukci kvantových jevů. Ve stejné době vytvořil Werner Heisenberg, Max Born a Pascal Jordan základy kvantové mechaniky atomových částic. Vycházel z představ Rutherforda, Bohra a Sommerfelda o stavbě atomu. Obě teorie byly popsány různou matematickou formou: Schrödingerovou vlnovou rovnicí a Heisenbergovými maticemi. Vznikla tak Schrödingerova vlnová mechanika a Heisenbergova maticová mechanika. Schrödinger už v roce 1926 ukázal formální rovnocennost obou návrhů. Na vzniku transformační teorie se pak podíleli především Paul Dirac a David Gilbert. Obě teorie sjednotili do kvantové mechaniky.
Heisenberg a Bohr ve své “Kodaňské interpretaci” z roku 1927 došli k závěru, že už volba mezi dvěma protiklady “částice nebo vlna” je falešná. Elektron není ani částice ani vlna. Při jeho popisu se však musí používat jak částicový model, tak také model vlnový. Systém pak existuje jako směsice různě pravděpodobných stavů až do chvíle, kdy pozorovatel ve svém experimentu jeden ze stavů vybere. Před pozorováním se světlo vyskytuje v obou stavech, je současně vlnou i částicí, dokud se nerozhodneme, kterou formu budeme měřit – poté světlo přijme jednu z těchto podob. Kodaňskou interpretaci se pokusil zesměšnit Erwin Schrödinger v článku z roku 1935, ve kterém přišel s myšlenkovým experimentem nazvaným Schrödingerova kočka. Pokusil se tak aplikovat pravidla vlnové a částicové povahy na reálný předmět. Snažil se zkritizovat to, že pozorování ovlivňuje chování objektu. „Kočka je uzavřená v ocelové schránce spolu s ďábelským zařízením (musí být zabezpečené před kočkou samotnou): v Geigerově čítači je malý kousek radioaktivní látky. Je tak malý, že v průběhu jedné hodiny existuje stejná pravděpodobnost, že se nějaký atom rozpadne, ale také stejná pravděpodobnost, že se nerozpadne žádný. Pokud dojde k rozpadu, v trubici čítače proběhne výboj, který sepne relé. Relé uvolní kladivo a to rozbije malou nádobku s kyselinou kyanovodíkovou. Pokud necháme systém hodinu o samotě, můžeme říct, že kočka stále žije, pokud se žádný atom nerozpadl. Jediný rozpad atomu by ale způpsobil smrt kočky.“ Když po hodině otevřeme schránku, je poměr pravděpodobnosti, že kočka žije a že je mrtvá 50:50. Schrödinger dále uvažoval v duchu kodaňské interpretace. Podle ní by kočka měla být před otevřením komory v neurčité superpozici obou stavů – měla by být současně živá i mrtvá. Stejně jako je vlnové nebo částicové chování elektronu fixováno na okamžik detekce, budoucnost kočky je předurčena pouze tím, že se rozhodneme otevřít schránku s kočkou a podívat se do ní. Podobně smýšlela i řada dalších vědců, kteří považovali kodaňskou interpretaci za směšnou.
S problémem určení fyzikálních veličin v definici a měření se zároveň klade otázka o vztahu klasické mechaniky a kvantové mechaniky. Odpověď na tuto otázku dává Bohrem vytvořený a Heisenbergem zpřesněný korespondenční princip. Ten požaduje, aby zákony kvantové fyziky přecházely v případě velkých kvantových čísel do zákonů klasické fyziky. Kvantová mechanika tím uzavírá klasickou mechaniku jako mezní případ a zároveň ohraničuje dosah její platnosti.
