Mnohoúhelník je část roviny ohraničená uzavřenou lomenou čárou, která se skládá z jednotlivých úseček, z nichž každé dvě sousední mají společný právě jeden krajní bod. Tyto body se nazývají vrcholy a pokud jich je n, pak hovoříme o n-úhelníku. Úsečka spojující dva nesousední vrcholy se nazývá úhlopříčka. Úhlopříčky existují v n-úhelníku pro n > 3 a platí, že počet úhlopříček je ½ ∙ n ∙ (n - 3).
Mnohoúhelníky mohou být konvexní a nekonvexní. Pokud leží spojnice libovolných dvou bodů mnohoúhelníku uvnitř mnohoúhelníku, pak se nazývá konvexní. Konvexní mnohoúhelník leží také vždy v jedné z polorovin určených kteroukoliv stranou. Součet velikostí všech vnitřních úhlů konvexního n-úhelníku se rovná (n – 2) ∙ 180°.
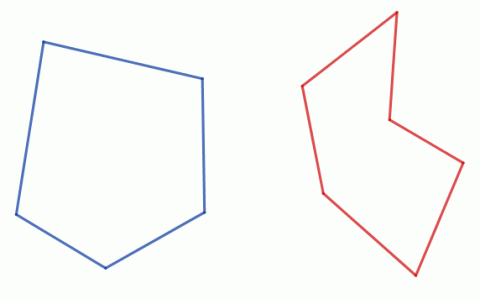
Konvexní (vlevo) a nekonvexní mnohoúhelník.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.
Pravidelné mnohoúhelníky
Pravidelný n-úhelník je mnohoúhelník, jehož všechny strany i vnitřní úhly jsou shodné. Pravidelný trojúhelník je rovnostranný trojúhelník, pravidelný čtyřúhelník je čtverec. Pravidelnému n-úhelníku lze opsat i vepsat kružnici. Je-li n sudé, existuje ke každému vrcholu protější vrchol, ke každé straně protější strana s ní rovnoběžná. Tyto mnohoúhelníky jsou osově a středově souměrné. Je-li n liché, přísluší ke každému vrcholu protější strana. Tyto mnohoúhelníky jsou jen osově souměrné.
Je-li a délka strany pravidelného n-úhelníku platí pro jeho obvod o
![]()
![]()
Pravidelný n-úhelník lze rozdělit na n rovnoramenných trojúhelníku se základnou a a výškou ρ, kde ρ je poloměr vepsané kružnice. Pro jeho obsah S proto platí
![]()
Pro obsah mnohoúhelníku s vrcholy v uzlech jednotkové čtvercové sítě platí Pickův vzorec, pojmenovaný po Georgu Pickovi, který byl pražským matematickým kolegou Alberta Einstein
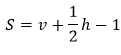
kde v je počet vnitřních a h počet hraničních bodů.
Hvězdicové mnohoúhelníky
Existují hvězdicové mnohoúhelníky, které vzniknou otočením pravidelného n-úhelníku o určitý úhel. Hvězdicové mnohoúhelníky jsou vždy nekonvexní.
Hvězdicový šestiúhelník a osmiúhelník.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.
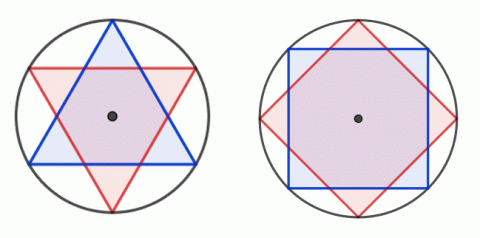
Pokud v pravidelném n-úhelníku spojíme každý vrchol s nesousedními vrcholy pak získáme další typ hvězdicového mnohoúhelníku.

Pentagram vznikne spojení každého vrcholu pětiúhelníku se dvěma nesousedními vrcholy.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.
Jedním z hvězdicových mnohoúhelníků je i pentagram (z řeckého pentagrammon – pět přímek). Odpradávna je mystickým symbolem, který poskytoval ochranu nebo naopak symbolizoval zlo. Pro Pythagorejce znamenal nekonečno, protože do vnitřního pětiúhelníku lze vpisovat další pentagramy. Pentagram byl symbolem bývalého Sovětského svazu, dnes se vyskytuje např. na státní vlajce Maroka a Etiopie. Tvar pentagramu má i hvězdice mořská.
Dalším v pořadí je hexagram, který vznikne spojením nesousedních vrcholů v šestiúhelníku. Tvar hexagramu měla třeba židovská hvězda.
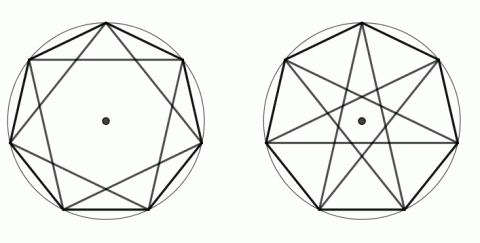
Dva typy hvězd získáme ze sedmiúhelníku.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.
Použité zdroje:
[1] FIALA, J. Hvězdicové mnohoúhelníky. Učitel matematiky, 2015, roč. 24, č. 1 (97), s. 29–45. ISSN 1210–9037.
