Pythagorova věta je asi nejslavnějším matematickým vzorcem. Dokonce se stala i součástí dnešní kultury, zmiňuje ji Homer Simpson nebo třeba Strašák v Čaroději ze země Oz. Věta pojmenovaná po řeckém Pythagorovi byla formulovaná již dříve Babyloňany a Číňany. Na babylonských hliněných tabulkách z 18. století před n. l se objevil součet 32 + 42 = 52. Používal se k vytyčování oltářů. Pythagoras nebo někdo z jeho školy zveřejnil první důkaz věty.
Pythagoras.
Zdroj: Techmania Science Center. Autor: Pavel Trnka. Under Creative Commons.
Pythagorova věta popisuje vztah mezi délkami stran libovolného pravoúhlého trojúhelníku v euklidovské rovině. Umožňuje dopočítat délku třetí strany takového trojúhelníka, pokud jsou známy délky dvou zbývajících stran. Věta zní:
Součet obsahů čtverců nad oběma odvěsnami se rovná obsahu čtverce nad přeponou.
Formálně Pythagorovu větu vyjadřuje rovnice
kde c označuje délku přepony pravoúhlého trojúhelníka a délky odvěsen jsou označeny a, b.
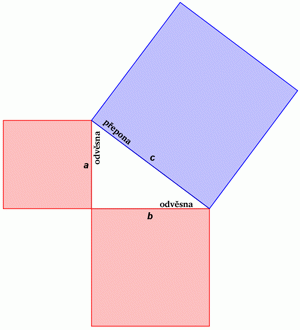
K odvození pythagorovy věty.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.
Čtverce v Pythagorově větě můžeme nahradit i jinými plošnými obrazci (kružnicí, obdélníkem, trojúhelníkem, pětiúhelníkem) za předpokladu, že jsou si navzájem podobné a jejich šířka je úměrná délce příslušné strany trojúhelníku. Součet obsahů těchto obrazců nad odvěsnami bude opět shodný s obsahem obrazce nad přeponou. Tuto myšlenku zveřejnil už Eukleides v 31. větě 6. knihy Základů.
Pythagorovu větu můžeme zobecnit pro obecný trojúhelník do tvaru tzv. kosinové věty
kde a, b, c jsou strany obecného trojúhelníku. Toto zobecnění znal už Eukleides, který ale nepoužíval funkci kosinus.
Lze Pythagorovu větu zobecnit tak, aby platilo a3 + b3 = c3 nebo a100 + b100 = c100 nebo obecně an + bn = cn? Tento problém sformuloval Pierre Fermat a snad jej i vyřešil. Na okraj Diofantovy knihy Arithmetica poznamenal: „Mám pro to skutečně nádherný důkaz, ale tento okraj je příliš úzký, než abych ho sem zapsal.“ Původní Fermatova kniha se nezachovala. O poznámce víme z výtisku, který vydal Fermatův syn i s otcovými poznámkami. Fermat měl na mysli to, že pro exponent větší než dvě žádné řešení neexistuje. Od té doby matematiky tento problém s názvem Velká Fermatova věta strašil. Postupně vznikly důkazy neexistence řešení pro jednotlivé exponenty, např. pro n = 3 vypracoval důkaz Leonhard Euler, pro n = 4 sám Fermat, pro n = 5 Peter Dirichlet. Ernst Kummer předložil důkaz pro všechna prvočísla menší než 100 s výjimkou čísel 37, 59 a 67. Kolem roku 1980 tak bylo dokázáno, že rovnost neplatí pro n od 3 do 125 000. Vzniklo dokonce nové odvětví – teorie čísel, které se problémem zabývá. Důkaz obecné věty však stále chyběl. Předloženo bylo několik tisíc důkazů, ale žádný správný. V roce 1908 vyhlásila Göttingenská akademie cenu 100 000 marek za její důkaz. Fermatovu hypotézu dokázal v roce 1994 Andrew Wiles. Důkaz je ale neuvěřitelně komplikovaný. I když samotná Velká Fermatova věta je jen jakousi kuriozitou bez praktického významu, tak metody použité k jejímu důkazu se staly zásadním a trvalým přínosem do matematické výzbroje.
Použité zdroje:
[1] BEUTELSPACHER, A. Matematika do vesty. Praha: Baronet, 2005. ISBN 80-7214-841-9.
[2] CRILLY, T. Matematika. 50 myšlenek, které musíte znát. 1. vydání. Praha: Slovart, 2010. ISBN: 978-80-7391-409-7.
[3] KUŘINA, F. Zobecnění pythagorovy věty aneb Jak odborný učitel Max Hlouba vyřešil Fermatův problém. Učitel matematiky, 2004, roč. 12, č. 2 (50), s. 65–73. ISSN 1210–9037.
[4] STEWART, I. Kabinet matematických kuriozit profesora Stewarta. Praha: Dokořán, 2013. ISBN: 978-80-7363-292-2.0.
