Kmitání

Třetím základním typem pohybu je kmitavý pohyb nebo také mechanické kmitání. Pro mechanické kmitání je charakteristické, že se těleso při pohybu neustále vrací do tzv. rovnovážné polohy. Jestliže těleso tento pohyb koná pravidelně, označujeme ho jako pohyb periodický (z řeckého peri = okolo a hodos = cesta). Jako periodický děj můžeme obecně nazvat jakýkoli děj, u něhož se pravidelně opakuje změna libovolné fyzikální veličiny (např. teplota, tlak, elektrické napětí, proud). Periodické pohyby konají např. části chvějící se struny na kytaře, písty spalovacího motoru, kyvadlo nástěnných hodin, srdce při pravidelné srdeční činnosti, blikající maják, závaží na pružině apod.

Zařízení, které volně kmitá bez vnějšího působení se nazývá mechanický oscilátor. Příkladem mechanického oscilátoru je kulička zavěšená na niti, která představuje kyvadlo. Volně zavěšené kyvadlo je v rovnovážné poloze. Kyvadlo se po vychýlení vrací do rovnovážné polohy, kde má největší rychlost a pokračuje dál v pohybu, až dosáhne největší výchylky. Tam se zastaví a vrací se zpět. Odtud je zřejmé, že kmitavý pohyb patří mezi pohyby nerovnoměrné.  Jestliže kyvadlo prošlo všemi naznačenými polohami, říkáme, že vykonalo jeden kmit.

          
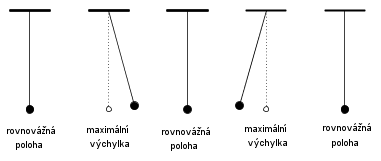
Průběh jednoho kmitu.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.

Závislost okamžité polohy kmitajícího tělesa na čase zobrazuje časový diagram, kde na vodorovné ose je čas a na svislé ose je okamžitá výchylka tělesa. Průběh kmitů můžeme sledovat osciloskopem.

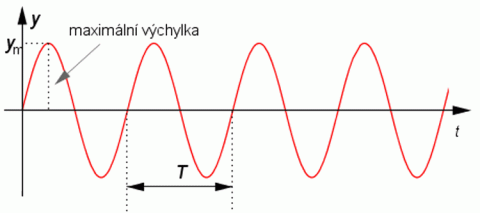
Veličiny popisující kmitavý pohyb.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.

Periodický pohyb je charakterizován pravidelným opakováním určitého pohybu. Nejkratší doba, za kterou dojde k opakování stejného pohybu, je perioda T. Perioda nezávisí na rozkmitu. Počet opakování stejného pohybu za časovou jednotku je frekvence nebo–li kmitočet f. Vztah mezi oběma veličinami

Jednotkou periody je sekunda. Jednotkou frekvence je hertz (Hz). Jeden hertz je frekvence periodického pohybu, jehož perioda trvá jednu sekundu. V praxi se častěji používají násobky – kilohertz kHz, megahertz MHz, gigahertz GHz.

Během jednoho kmitu se kulička nepohybuje rovnoměrně. Při přemísťování z krajní polohy do polohy rovnovážné koná pohyb zrychlený, při přemísťování z rovnovážné polohy do polohy krajní pohyb zpomalený. Rovnovážnou polohou prochází kulička největší rychlostí. V krajních polohách se na okamžik zastaví.

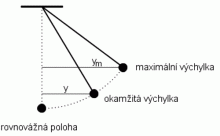
Okamžitá a maximální výchylka.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.

V každém okamžiku můžeme měřit vzdálenost kuličky od rovnovážné polohy, tzv. okamžitou výchylkou y. Největší okamžitá výchylka je amplituda výchylky y_m nebo zkráceně jen amplituda. Z časového diagramu je patrné, že se okamžitá výchylka mění s časem podle funkce sinus. Kmitavý pohyb, jehož časovým diagramem je sinusoida (popř. kosinusoida) se nazývá harmonický kmitavý pohyb nebo harmonické kmitání. Je to jeden z nejjednodušších kmitavých pohybů. V přírodě i technické praxi mají kmitavé pohyby složitější průběh, nazývají se pak neharmonické. Rovnice pro okamžitou výchylku při harmonickém pohybu můžeme napsat ve tvaru

Úhel ωt nazýváme fáze harmonického pohybu a veličinu ω úhlová frekvence. Dále můžeme určit rychlost kmitavého pohybu

Je vidět, že rychlost je také periodickou funkcí času, ale mění se podle funkce kosinus, tj. při nejmenší výchylce je rychlost největší, naopak při největší výchylce je rychlost nejmenší (tedy nulová). Další kinematickou veličinou, kterou můžeme určit, je zrychlení

Zrychlení je přímo úměrné okamžité výchylce a v každém okamžiku má opačný směr. Pro lepší pochopení je v následujícím grafu modře vyznačen časový průběh výchylky kmitů, zeleně rychlosti a červeně zrychlení.

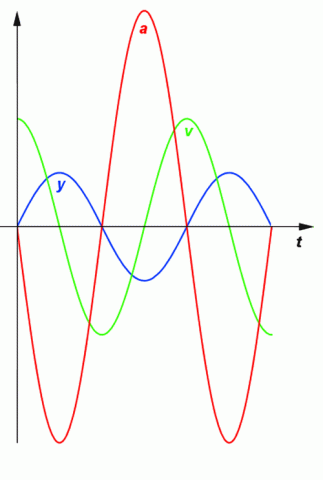
Fázový posun vektoru okamžité výchlky, rychlosti a zrychlení.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.

Vztahy pro okamžitou výchylku, rychlost a zrychlení platí jen tehdy, jestliže měříme od okamžiku, kdy kmitající bod prochází rovnovážnou polohou. Často měříme harmonický pohyb od okamžiku, kdy kmitající bod neprochází rovnovážnou polohou. Okamžitou výchylku pak vyjádříme vztahem

kde fázi harmonického pohybu představuje výraz ωt + φ, přičemž veličinu φ nazýváme počáteční fáze harmonického pohybu. Tento vztah je obecnou rovnicí harmonického kmitání.

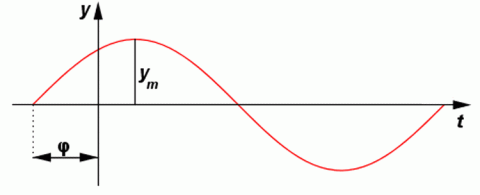
Fáze harmonického pohybu.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.

Počáteční fáze má význam zejména při sledování dvou harmonických pohybů. Např. v autoopravnách se při testování činnosti spalovacího motoru vyšetřuje vzájemný pohyb dvou pístů, přičemž se určuje tzv. fázový rozdíl, což je rozdíl počátečních fází pohybů. Jsou–li okamžité výchylky dvou harmonických kmitání y₁ = y_m1sin(ωt + φ₁) a y₂ = y_m2sin(ωt + φ₂), pak fázový rozdíl jejich kmitání je Δφ = φ₁ − φ₂. Důležitý případ nastane, když je fázový rozdíl roven nule nebo sudému násobku π – oba harmonické pohyby mají stejnou fázi, nebo když je fázový rozdíl roven lichému násobku π – oba harmonické pohyby mají opačnou fázi.