Složené kmitání

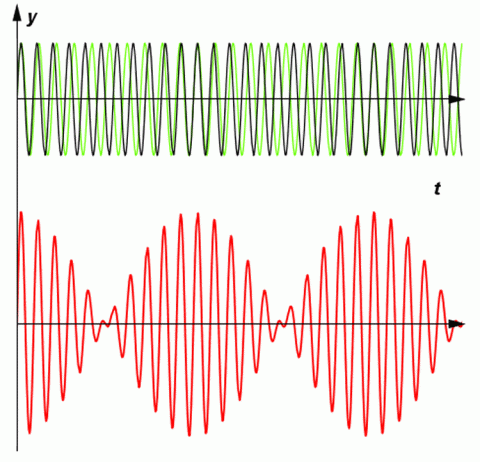
Působí–li na mechanický oscilátor současně dvě síly, z nichž každá může vyvolat samostatný harmonický pohyb oscilátoru, oba pohyby se skládají a vzniká výsledný pohyb, který nazýváme složené kmitání.

Složené kmitání může mít různý průběh. V jednoduchých případech má průběh harmonický, v ostatních případech neharmonický, i když oba skládané pohyby jsou harmonické. Mají–li oba oscilátory stejné parametry, pak harmonické kmitání obou oscilátorů má stejnou frekvenci a výsledné kmitání je také harmonické. Při nestejných parametrech oscilátorů je jejich frekvence různá a výsledné kmitání je sice periodické, ale ne harmonické.

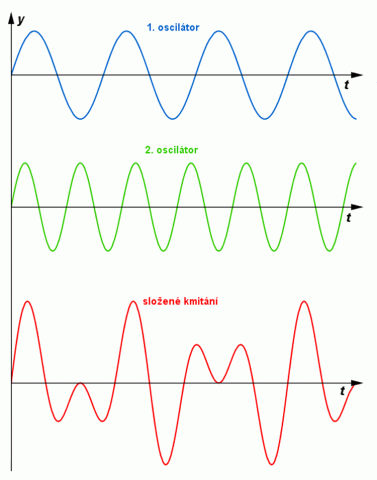
Grafické skládání kmitání.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.

Zjišťování výsledného kmitání matematickými postupy je poměrně složité, zvláště při různých frekvencích, amplitudách a počátečních fázích skládaných harmonických pohybů. Obecně platí princip superpozice: Koná–li hmotný bod současně dva nebo více harmonických pohybů v jedné přímce s okamžitými výchylkami y₁, y₂, …, je okamžitá výchylka výsledného kmitání

Skládáním dvou harmonických kmitání stejného směru a stejné frekvence vzniká opět harmonické kmitání stejné frekvence. Jeho amplituda závisí na fázovém rozdílu složek.

Skládání dvou kmitání se stejnou periodou.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.

Jestliže fázový rozdíl Δφ = 0 (při stejné počáteční fázi obou složek), je amplituda složeného kmitání největší. Složené kmitání má stejnou počáteční fázi jako složky. Je–li fázový rozdíl Δφ = π (při opačné fázi obou složek), je amplituda výsledného kmitání nejmenší. Složené kmitání má stejnou počáteční fázi jako složka s větší amplitudou. V případě stejných amplitud je výchylka nulová a kmitání zaniká.

Superpozicí kmitání různé frekvence, tzn. když f₁ ≠ f₂, vzniká složené kmitání, které není harmonické. Kmitání však může být periodické a to v případě, že v poměru jejich period, popř. frekvencí, jsou celá čísla (viz první obrázek tohoto článku, kde jsou frekvence v poměru 3:5).

Výchylka bodu, který koná zároveň několik různosměrných kmitů, je podle principu superpozice v každém okamžiku vektorovým součtem jednotlivých výchylek. Mají–li dílčí kmity souměřitelné periody, opakuje se vždy pohyb po určité době znovu a znovu; je to zase periodický kmit, který obecně probíhá prostorovou uzavřenou křivkou. Nejsou–li periody souměřitelné, je výsledný kmit neperiodický, pohyb se neopakuje přesně stejným způsobem. Při skládání dvou kmitů probíhajících v přímce se souměřitelnými periodami (v poměru malých celých čísel), dostaneme poměrně jednoduché křivky, nazývané podle svého objevitele, profesora fyziky na lyceu Saint–Louis v Paříži, Julesa A. Lissajouse – Lissajousovy obrazce. Poprvé o nich psal v roce 1857 v obsáhlé publikaci Mémiore sur l´étude optique des mouvements vibratoires (O zkoumání optickém pohybů kmitových).

Při poměru kmitů 1:1 dostáváme rovnici

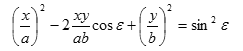
kde a, b jsou amplitudy skládaného kmitání a ε je fázové posunutí.

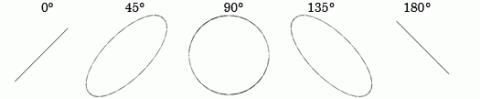
Lissajousovy obrazce při poměru kmitů 1:1.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.

Při poměru 2:1 dostaneme pro výsledné kmitání rovnici

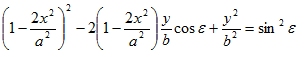
a průběh kmitů

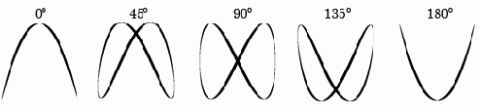
Lissajousovy obrazce při poměru kmitů 2:1. Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.

Při poměru 3:1

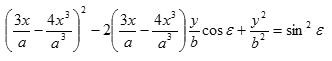
a průběh kmitů

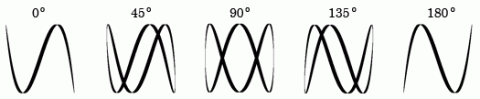
Lissajousovy obrazce při poměru kmitů 3:1.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.

Zvláštní případ nastává, když se frekvence složek velmi málo liší. Z dalšího obrázku je patrné, že amplituda výsledného kmitání se periodicky zvětšuje a zmenšuje. Vzniká složené kmitání, které nazýváme rázy neboli zázněje. Počet rázů za sekundu se řídí rozdílem frekvencí obou kmitání

Pro stejné frekvence rázy zaniknou. Rázy jsou velmi citlivým indikátorem pro sladění dvou současně znějících tónů. Vymizí–li rázy, jsou oba tóny dokonale sladěny.

Vznik rázů graficky.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.

Jean Fourier dokázal, že každý periodický pohyb lze rozložit obecně na nekonečně mnoho harmonických kmitů, jejichž frekvence jsou v jednoduchém poměru přirozených čísel. Tyto frekvence jsou celistvými násobky základní frekvence zkoumaného kmitání. Celý proces vyšetřování kmitání se nazývá harmonická nebo Fourierova analýza.

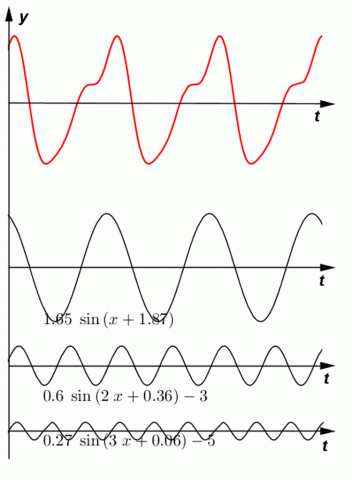
Fourierova analýza graficky.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.