Vhodíme–li na klidnou vodní hladinu rybníka kámen, hladina se jeho dopadem rozkmitá a z místa rozruchu se začnou šířit kruhové vlny. Jako vlnění označujeme šíření kmitavého rozruchu prostředím. Vlněním se přenáší pouze energie, částice kmitají, ale nepřemísťují se, kmitají kolem své rovnovážné polohy. Důkazem je např. plovoucí listí na rozvlněné hladině vody. Po hladině se sice šíří vlny, ale listí zůstává na místě (platí to samozřejmě jen pro malé vlnky). Místo, z něhož se rozruch šíří, se nazývá zdroj vlnění.
Příčinou mechanického vlnění je existence vazeb mezi částicemi (atomy, molekulami) prostředí, kterým se vlnění šíří. Kmitání jedné částice se vzájemnou vazbou přenáší na další částici. Současně se na tuto částici přenáší energie kmitavého pohybu. Říkáme, že se prostředím šíří postupné vlnění. Pro zjednodušení se budeme zabývat vlněním, které se šíří jen v jednom směru. Jednotlivé částice si představíme jako řadu bodů vzájemně vázaných pružnými silami. Při postupném vlnění se pohybují všechny částice prostředí. Každá z nich dosahuje postupně amplitudy výchylky a pak je zase v určitém okamžiku v klidu.
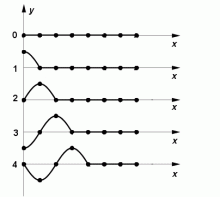
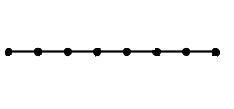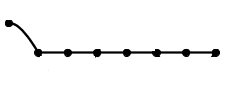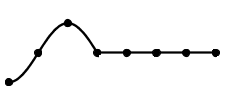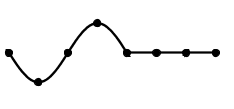
Vznik postupného vlnění příčného a podélného.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.
Směr kmitání jednotlivých částic je kolmý na směr šíření vlnění, tento druh vlnění se označuje jako postupné příčné – transversální. Je charakteristické tím, že se prostředím šíří vrh a důl vlny. Takové vlnění se nazývá také lineárně polarizované. Obecně může bod opisovat jakoukoli Lissajousovu křivku ve směru příčném. Pak se jedná o vlnění nepolarizované. Jestliže částice budou kmitat ve směru šíření, vznikne vlnění postupné podélné – longitudinální. Podélné vlnění charakterizuje zhuštění a zředění částic v bodové řadě. Protože jsou amplitudy výchylek jednotlivých částic velmi malé a jejich směr splývá se směrem šíření vlnění, není většinou podélné vlnění přímo pozorovatelné (šíření zvuku ve vzduchu).
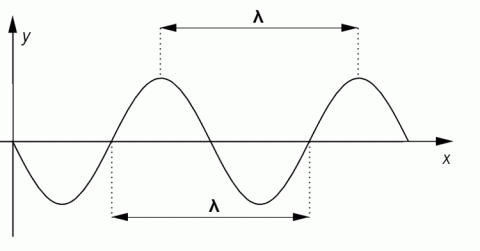
Mechanické vlnění se šíří jen pružným prostředím a jeho rychlost závisí na druhu prostředí. Dráhu, kterou vlnění proběhne za jednu periodu, nazveme vlnová délka. Vlnová délka je obecně vzdálenost kterýchkoli dvou nejbližších bodů, které kmitají se stejnou fází. Body ve vzdálenosti poloviny vlnové délky kmitají s opačnou fází. Pro vlnovou délku platí obdoba vztahu pro dráhu rovnoměrného přímočarého pohybu s = vt.
kde f je frekvence vlnění, což je frekvence kmitání jak počátečního bodu řady, tak všech ostatních bodů řady, k nimž kmitavý rozruch dospěje, λ vlnová délka a v rychlost šíření.
Vlnová délka.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.
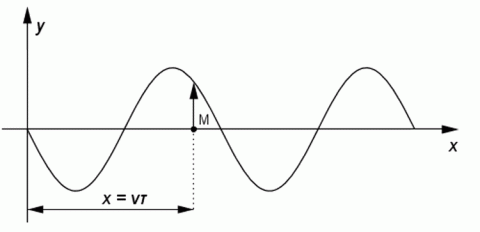
Uvažujme opět řadu bodů, jejíž počáteční bod uvedeme do kmitavého pohybu. Je–li jeho kmitání harmonické, mění se okamžitá výchylka v závislosti na čase podle vztahu y = ymsin ωt, kde ym je amplituda výchylky a ω úhlová frekvence kmitání. Jsou–li částice bodové řady vzájemně vázány pružnými silami, kmitání se přenáší od počátečního bodu postupně na další částice a bodovou řadou se šíří postupné vlnění. Do určitého bodu M bodové řady, který leží ve vzdálenosti x od počátečního bodu, dospěje vlnění při rychlosti v za dobu τ = x/v. O tuto dobu začne bod M kmitat později než počáteční bod.
Proto okamžitá výchylka bodu M je
Dostáváme rovnici postupné vlny, která vyjadřuje závislost okamžité výchylky libovolné kmitající částice bodové řady jednak na čase t, který měříme od okamžiku průchodu počátečního bodu řady rovnovážnou polohou, jednak na vzdálenosti x částice od počátečního bodu, který je zdrojem vlnění. Okamžitá výchylka částice bodové řady je funkcí dvou proměnných: času a vzdálenosti místa od zdroje vlnění. Proto říkáme, že postupné vlnění je periodický děj v prostoru a čase. Dosadíme–li do rovnice za úhlovou rychlost a vlnovou délku, dostáváme rovnici postupné vlny ve tvaru
Obě rovnice pro okamžitou výchylku platí jak pro postupné vlnění příčné, tak pro postupné vlnění podélné. U postupného vlnění podélného představuje kladná výchylka výchylku vpravo a záporná výchylka výchylku vlevo.
