Kyvadlo

Kyvadlo (latinsky corpus pendulum – těleso visící) sehrálo významnou úlohu v historii měření času jako jednoduché zařízení, jehož periodu kmitání lze snadno a poměrně přesně nastavit změnou jediného parametru, kterým je délka kyvadla. Konstrukcí mechanizmu kyvadlových hodin proslul holandský fyzik Christian Huygens. Kyvadlem může být každé tuhé těleso otáčivé kolem vodorovné osy umístěné nad jeho těžištěm, takové kyvadlo nazýváme fyzické. Kmitavý pohyb kyvadel, které mají různý tvar a hmotnost, je poměrně složitý. Proto zavedeme jednoduchý model kyvadla, kterým je matematické kyvadlo, jehož závěs je nehmotný. Přibližně ho realizujeme zavěšením malé těžší kuličky na tenkou pevnou nit, jejíž hmotnost je zanedbatelně malá vzhledem k hmotnosti kuličky.

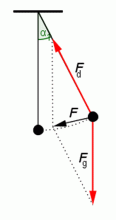
Síly působící na kyvadlo.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.

Po sestavení příslušných rovnic a při podmínce malé výchylky vzhledem k délce závěsu, můžeme psát

Pro frekvenci a periodu kmitání matematického kyvadla můžeme z tohoto vztahu odvodit

Frekvence a perioda harmonického pohybu matematického kyvadla při malé výchylce závisí na délce jeho závěsu a na velikosti tíhového zrychlení v daném místě. Proto délka sekundového kyvadla není na všech místech Země stejná, liší se až o 6 mm.

Frekvence a perioda nezávisí na hmotnosti kyvadla ani na jeho rozkyvu (jen pokud je úhel rozkyvu malý). Tato myšlenka je už velmi stará, své počátky má snad už v Číně, ve starém Řecku, u Mikuláše z Oresme, Leonarda da Vinci, Girolama Cardana a dalších. První vědecký popis se objevil někdy v roce 1583 nebo 1584 od Galilea Galilei, ten na tuto závislost přišel pravděpodobně při pozorování lustrů v pisánském chrámu během bohoslužeb, ale bohužel se ve svých výpočtech mýlil. Správný výsledek zveřejnil až v roce 1687 Isaac Newton. Zákonitost ověřil při pokusu se stejně dlouhými kyvadly, jejichž duté kuličky byly z různých látek, ale měly stejný objem (aby byl odpor vzduchu stále stejný). Všechna kyvadla se kývala stejně. Při malých rozkyvech nezávisí doba kyvu na velikosti rozkmitu. Mezi další pokračovatele patřil Christian Huygens, Leonhard Euler, Simeon Poisson, Adrien Legendre nebo Carl Jacobi. Huygens při konstrukci hodin usiloval o to, aby doba kyvu nezávisela na rozkyvu. Proto hodiny doplnil dvěma plíšky, které umístil do blízkosti závěsu. Plíšky omezovaly vlákno při větších rozkyvech a konec závěsu neopisoval část kružnice, ale cykloidy.

Galileo Galieli.
Zdroj: Techmania Science Center. Autor: Pavel Trnka. Under Creative Commons.

Místo periody neboli doby kmitu T se častěji používá doba kyvu τ, která se rovná polovině jeho doby kmitu.

Ze vztahu pro zrychlení kmitavého pohybu a z druhého Newtonova zákona můžeme sestavit rovnici pro sílu způsobující harmonický pohyb tělesa o hmotnosti m

Pohyb harmonický vzniká tehdy, působí–li na hmotný bod síla úměrná okamžité výchylce a směřující k rovnovážné poloze hmotného bodu, má tedy opačný směr než výchylka y. Pro kmitavý pohyb na pružině můžeme v rovnici nahradit mω² = k a rovnici pro sílu pružnosti přepsat do tvaru

kde k je tuhost pružiny, jejíž hodnota závisí na tloušťce pružinového drátu, na materiálu, z něhož je vyroben a na průměru pružiny. Pro úhlovou rychlost pak platí

Po dosazení za úhlovou frekvenci dostaneme pro periodu a frekvenci kmitání závaží na pružině vztahy

Odtud jasně plyne, že frekvence a perioda závisí jen na hmotnosti kmitajícího bodu a tuhosti pružiny. Stejnou situaci můžeme rozebrat i pro kyvadlo. Na kuličku působí tíhová síla a síla namáhající závěs. Obě síly jsou kompenzovány silou harmonického kmitání. Celou situaci názorně představuje animace, kde tíha je w, síla namáhající závěs T a výsledná síla s.

Reálná kyvadla používaná v praxi jsou kyvadla fyzická. Periodu fyzického kyvadla určujeme měřením. Mezi další druhy kyvadel patří např. sférické kyvadlo (kývá současně ve dvou směrech, koná kruhové nebo eliptické kmity), reversní kyvadlo (je kyvadlo se dvěmi rovnoběžnými osami, které jsou nesouměrně položeny vzhledem k těžišti a pro něž je doba kyvu kyvadla stejná. Používá se k určení gravitačního zrychlení) balistické kyvadlo (používá se k balistickým měřením, torzní (hybnou silou je kroucení závěsného vlákna, perioda závisí na délce vlákna, na jeho průměru a materiálu) nebo Foucaultovo kyvadlo.