Šíření vlnění v prostoru

Rychlost, kterou se vlnění šíří v prostoru, závisí na fyzikálních vlastnostech prostředí, např. na pružnosti a hustotě prostředí. Jsou–li fyzikální vlastnosti prostředí ve všech směrech stejné, je také ve všech směrech stejná velikost rychlosti vlnění. Takové prostředí nazýváme izotropní prostředí.

Stane–li se určitý bod prostředí, např. vzduch, zdrojem kmitavého rozruchu, postupuje vlnění ze zdroje všemi směry rychlostí v a za dobu t dosáhne vzdálenosti r = vt. Všechny body, do nichž dospěje vlnění z bodového zdroje za stejnou dobu, leží na kulové ploše, kterou nazýváme vlnoplocha. Všechny body stejné vlnoplochy kmitají se stejnou fází. Směr šíření vlnění určuje přímka, která vychází ze zdroje vlnění kolmo na vlnoplochu a nazývá se paprsek. V blízkosti bodového zdroje vlnění se vytvářejí kulové vlnoplochy. Ve větších vzdálenostech od zdroje je však zakřivení kulových vlnoploch tak malé, že můžeme jejich části nahradit vlnoplochami rovinnými.

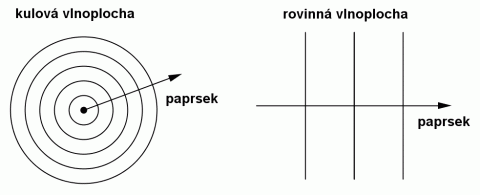
Kulová a rovinná vlnoplocha.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.

Vzbudíme–li v pevném tělese výchylku určitého směru, šíří se v jejím směru podélná vlna, ve směrech kolmých k směru původní výchylky se šíří vlna příčná. Obě vlny se šíří různou rychlostí, podélná rychleji. V kapalinách a plynech se příčné vlny nešíří. Kapalinami a plyny mohou tedy postupovat jen vlny podélné.

Obecně pro šíření vlnění v libovolném pružném prostředí platí tzv. Huygensův princip, který zformuloval v roce 1678 Christian Huygens a vydal v roce 1690 ve spise Traité de la lumiere, ou sont expliquees les causes de ce dui luy arrive dans la reflexion et dans la refractions et particulierement dans l´etrange refractions du cristal d´Islande: Každý bod vlnoplochy, do něhož dospěje vlnění v určitém okamžiku, se stává zdrojem nového, tzv. elementárního vlnění, které se šíří z tohoto zdroje v elementárních vlnoplochách. Vnější obalová plocha všech elementárních vlnoploch tvoří výslednou vlnoplochu v dalším časovém okamžiku.

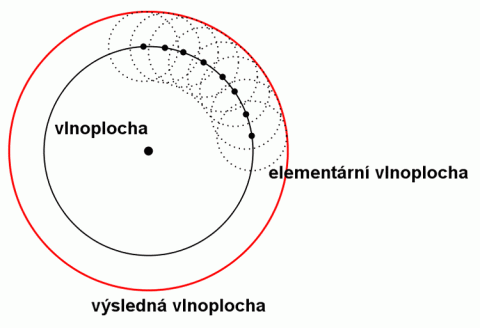
Vznik další vlny podle Huygense.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.

Význam Huygensova principu je patrný z obrázku. Vlnění, které se šíří z bodového zdroje dospěje do určité vzdálenosti a vytvoří kulovou vlnoplochu. Každý bod této vlnoplochy, který je zdrojem nového vlnění, vytvoří elementární vlnoplochu. Huygensův princip doplnili Augustin Fresnel a Gustav Kirchhoff. Ukázali a vysvětlili, že účinek elementárních vlnoploch se projevuje právě na vnější obálce. Příčinou je interference elementárních vln, které se zesilují právě jen na vnější obálce a dávají tak vzniknout výsledné vlnoploše. Huygensův princip doplněný tímto poznatkem se nazývá Huygensův – Fresnelův. Pomocí Huygensova principu můžeme konstruovat vlnoplochy v každém dalším okamžiku šíření vlnění, známe–li polohu některé vlnoplochy v okamžiku předcházejícím, a to i tehdy, jestliže neznáme polohu zdroje vlnění.

Příkladem může být šíření mechanického vlnění na vodní hladině. Jestliže použijeme překážku s malým otvorem, pak se za otvorem vytvářejí nové vlny tak, jako kdyby byl otvor zdrojem vlnění.

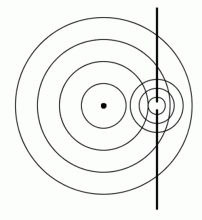
Šíření vlnění za malým otvorem.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.

Na základě Huygensova principu můžeme vysvětlit, proč za lodí vzniká rozšiřující se brázda. Oba přímé okraje brázdy jsou obálkou kruhových vlnoploch s poloměry rostoucími úměrně s časem, a tedy i se vzdáleností od rovnoměrně plující lodi.

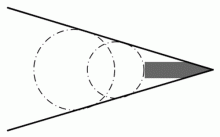
Vznik brázdy za lodí.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.

Úhel brázdy φ závisí na poměru rychlosti šíření vln v_φ a pohybu lodi v_z

Problém můžeme zobecnit pro pohyb libovolného tělesa rychlostí v_z v prostředí, kterým se vlny šíří rychlostí vφ (např. zvuk ve vzduchu). Při pohybu tělesa menší rychlostí než jakou se šíří vlny ke vzniku kýlové vlnoplochy nedojde, vlnoplochy předbíhají těleso. Blíží–li se rychlost tělesa rychlosti šíření vln v daném prostředí, začíná se tekutina stlačovat, hromadí se před tělesem a její hustota se značně zvětšuje. Odpor prostředí za této situace prudce roste, neboť lokální „zhuštění“ tekutiny před tělesem se nestačí přenést do okolí. Před tělesem se tak vytváří tzv. tlaková (zvuková) bariéra, tlačená tělesem dopředu.

Letadlo a střela pohybující se nadzvukovou rychlostí.
Zdroj: www.nasa.gov.

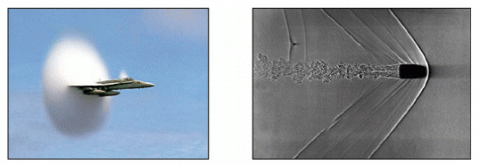
Při pohybu tělesa rychlostí větší než jakou se šíří vlny vzniká rázová vlna, jejíž tvar závisí na tvaru pohybujícího se tělesa. Při překonávání tlakové bariéry dochází k vyrovnání velmi rozdílných tlaků před a za tělesem, provázeném zvukovými efekty značné intenzity. Značná část energie pohybu se spotřebuje na vznik zvukových a rázových vln. Když rázová vlna dosáhne k zemskému povrchu, vnímáme ji sluchem jako silnou ránu podobající se výstřelu. Tento zvuk označujeme jako akustický třesk. Vznik akustického třesku je jedním z důvodů, proč se letadla mohou pohybovat nadzvukovou rychlostí jen ve velkých výškách. Akustický třesk je tím intenzivnější, čím se těleso pohybuje rychleji. Je–li přední část tělesa zaostřená, pak čelo vzniklé rázové vlny má tvar kužele, přičemž zaostřený hrot tělesa je společný s vrcholem kužele. Má–li těleso tupý předek, pak vzniklá rázová vlna je odtržená od tělesa a šíří se před ním. U rozlehlého tělesa vzniká kromě přední zhuštěné rázové vlny ještě vlna zadní zředěná. Mezi těmito vlnami mohou vzniknout ještě dílčí kýlové vlny.

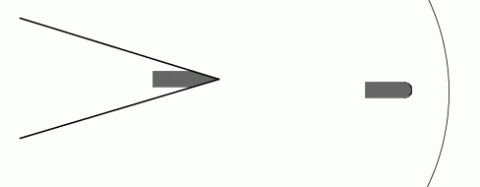
Vznik vlny při pohybu tělesa podzvukovou a nadzvukovou rychlostí.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.

Ke vzniku rázové vlny dochází například při výbuších, jiskrových výbojích nebo při letu střely (viz předchozí obrázek), letadla či rakety nadzvukovou rychlostí ve vzduchu, při termonukleárních reakcích v přehřáté plazmě.