Nakloněnou rovinu známe z běžného života, aniž bychom si uvědomovali, že se jedná o jednoduchý stroj, třeba v zimě při sáňkování a lyžování. Její princip znali už staří Egypťané a umožnil jim stavbu pyramid a chrámů. Nakloněnou rovinu využíváme k usnadnění chůze nebo jízdy do výšky, ale také ke spouštění břemen nebo při jízdě z kopce. Princip nakloněné roviny je součástí řady strojů a nástrojů, nejčastěji v podobě klínů a šroubů.
Nakloněná rovina.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.
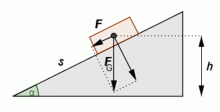
Pro rovnováhu na nakloněné rovině, jestliže na těleso působí síla F, platí
kde G je tíha tělesa. Nakloněnou rovinou se zabýval i Simon Stevin, který princip nakloněné roviny vysvětlil pomocí řetězu z koulí.
Nakloněná rovina.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.
Nakloněnou rovinu znázornil pomocí trojúhelníku, na který ovinul řetěz bez konce. Řetěz buď v rovnováze není a bude se donekonečna pohybovat (pak by to bylo perpetuum mobile) nebo v rovnováze je, a pak je ale v rovnováze i samotná část vysícího řetězu a po jeho odstranění se neporuší ani rovnováha části ABC. Část BA řetězu je přesně vyvážena částí BC. Tento obrázek se objevil na titulní stránce jeho hlavního díla Wonder en si gheen wonder (Div, a přece ne div). Odtud také pochází zlaté pravidlo mechaniky: Co se ztratí na dráze, to se musí přidat na síle. Ze schématu nakloněné roviny je patrné, že pro zdvižení tělesa po dráze s je při působení síly F třeba práce W = Fs = mgh, kde h je výška nakloněné roviny. Rovnost
pak představuje vztah pro rovnovážnou polohu na nakloněné rovině.
