Řešení úloh pomocí rovnic se objevilo na babylonských hliněných destičkách z doby 2000 před n. l., na egyptských papyrech nebo v čínských výpočtech. Babyloňané řešili rovnice prvního a druhého stupně a s pomocí tabulek i některé druhy rovnic třetího stupně. Al-Chwárizmí napsal na počátku 9. století Al-Kitáb al-muchtasar fi hisáb al–džebr wa–l–muqábala (Krátká kniha o počtu algebry a al–muqábaly). Al-džebr znamená změnu odčítaného (v dnešním smyslu záporného) čísla v číslo kladné, když se převede z jedné strany rovnice na druhou. Protože v té době se záporná čísla nepokládala za skutečná čísla, zdála se operace al-džebr jako zázrak. Kniha byla ve 12. století přeložena do latiny a byla předlohou evropských učebnic algebry. Algebra byla dlouho nazývána velkým uměním vedle malého umění aritmetiky. Výraz algebra se u Arabů používal i v medicíně – znamenal narovnávání kostí zlámané ruky nebo nohy. Algebrista je tedy nejen znalec algebry, ale i lékař.
Algebraickou symboliku používali už matematikové v Babylonu, kteří v textech používali zvláštní značku pro neznámé hledané číslo. Ve 3. století n. l. Diofantos používal v díle Aritmetika symboly pro neznámou i pro označneí jejích mocnin, používal pouze operace sčítání a odčítání, vztah rovnosti a neznámou s jejími mocninami. Ostatní hodnoty v rovnici se vyjadřovaly konkrétními čísly, slovy nebo celými větami. Řešil rovnice třetího a čtvrtého stupně. Matematikové, kteří psali arabsky, nazývali hledané neznámé číslo „věcí“, ale nepoužívali speciální symbol. Z prvního písmena tohoto slova v evropské transkripci vzniklo označení neznámé písmenem x. Francois Viete zavedl pro obecná čísla velká písmena: pro neznámé samohlásky, pro známé hodnoty souhlásky. S dnešní symbolikou se setkáváme – až na malé odchylky – u René Descarta. Zavedení vhodné symboliky proměnných se stalo nástrojem obrovského rozvoje matematiky.
Druhy rovnic a jejich řešení
Rozlišujeme několik typů rovnic s jednou neznámou. Jedním z kritérií je stupeň rovnice, tj. nejvyšší mocnina, která se v rovnici vyskytuje. Z roku 1629 pochází tzv. základní věta algebry, kterou formuloval Albert Girard: obecná algebraická rovnice o jedné neznámé má tolik kořenů, jakého je stupně. Kořeny mohou být reálné i imaginární
Nejnižší stupeň jedna má rovnice lineární (např. 3x – 2 = 0, obecně ax + b = 0), která má řešení ve tvaru x = -b/a. Rovnice druhého stupně se nazývá kvadratická (např. 3x2 - 2x + 1 = 0, obecně ax2 + bx + c = 0) a má řešení ve tvaru
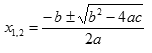
Rovnice třetího stupně se nazývají kubické (např. 3x3 – x2+ 2x - 4 = 0, obecně ax3 + bx2 + cx + d = 0) a její řešení objevil nejprve Scipione del Ferro a pak Niccolo Tartaglia. Dnes se vzorce pro řešení kubické rovnice nazývají Cardanovy a jsou poměrně složité. Rovnice čtvrtého řádu, které se nazývají kvartické, jsou řešitelné pomocí složitých vzorců. Niels Abel a Evariste Galois dokázali, že rovnice vyšších řádů už nejsou řešitelné dosazením do nějakého vzorce. K nalezní řešení rovnic vyššího řádu je nutné použít jiné metody (např. postupy numerické matematiky nebo grafické řešení). Jedním ze speciálních typů rovnic vyšších řádů je rovnice xn - 1 = 0, která má n reálných nebo komplexních kořenů. Zajímavostí je, že všechny kořeny tvoří v gaussově komplexní rovině pravidelný n-úhelník (např. rovnice x4 – 1 = 0 má dva reálné kořeny 1 a -1 a dva komplexní kořeny, které při znázornění do gaussovy roviny tvoří čtverec).
Použité zdroje:
[1] BEUTELSPACHER, A. Matematika do vesty. Praha: Baronet, 2005. ISBN 80-7214-841-9.
[2] DEPMAN, I. Besedy o matematice. Praha: Státní pedagogické nakladatelství, 1957.
[3] MRÁZEK, J. Taje matematiky. Praha: Práce, 1986. ISBN 24-025-86.
[4] MÜLLEROVÁ, J. Matematika pro 8. ročník 1. díl. Praha: Státní pedagogické nakladatelství, 1990. ISBN 80-04-24008-9.

