O číslech 35 a 5 se můžeme vyjádřit tak, že číslo 35 je násobkem čísla 5 nebo že číslo 5 je dělitelem čísla 35. Obecně platí, že pro každé přirozené číslo existují dva dělitelé, tedy čísla, kterými se dá číslo dělit. Je to vždy číslo jedna a stejné číslo. Obě čísla se nazývají samozřejmí dělitelé. Abychom snadno našli dělitele daného čísla, můžeme použít následující znaky dělitelnosti.
|
2 |
číslo je sudé, tj. má poslední číslici 0, 2, 4, 6, 8 |
|
3 |
ciferný součet dělitelný třemi |
|
4 |
poslední dvojčíslí je dělitelné čtyřmi |
|
5 |
zápis čísla končí na 0 nebo 5 |
|
6 |
je dělitelné dvěma a zároveň třemi |
| 7 | jednotlivé cifry vynásobíme řadou čísel 1, 3, 2, 6, 4, 5 a to tak, že začínáme u jednotek, pokud řada čísel nestačí, tak ji použijeme znovu, jednotlivé součiny sečteme a součet musí být dělitelný sedmi |
|
8 |
poslední trojčíslí je dělitelné třemi |
|
9 |
ciferný součet je dělitelný devíti |
|
10 |
zápis čísla končí nulou |
|
11 |
součet číslic lichých řádů je roven součtu číslic sudých řádů anebo se tyto součty liší o násobek jedenácti |
|
12 |
dělitelné třemi a čtyřmi |
|
13 |
číslo rozdělíme zprava na trojčíslí. Odečteme vždy ta čísla na lichých místech od těch na sudých místech (lze i obráceně), výsledek je dělitelný 13 |
|
14 |
dělitelné dvěmi a sedmi |
|
15 |
dělitelné třemi a pěti |
|
19 |
číslo ve tvaru 100a + b, pak je dělitelné 19 číslo a + 4b |
V souvislosti se zjištěním dělitelů daného čísla, rozlišujeme několik zajímavých čísel. Prvočísla jsou všechna přirozená čísla, která mají pouze samozřejmé dělitele, číslo jedna a samo sebe. Opakem jsou složená čísla, která mají aspoň tři různé dělitele. Číslo jedna nepovažujeme ani za prvočíslo, ani za složené číslo. Existují i vysoce složená čísla, která takto označil Srinivasa Ramanujan. Označil tak čísla, která mají více dělitelů než všechna ostatní čísla. Prvním vysoce složeným číslem je 36, které má dělitele: 1, 2, 3, 4, 6, 9, 12, 18 a 36. Žádné číslo od 1 do 35 jich tolik nemá. Další vysoce složené číslo je 332 640, 43 243 200 nebo 2 248 776 129 600.
Jestliže součet dělitelů jednoho čísla dává druhé číslo a naopak, pak se čísla nazývají spřátelená (např. 48 má dělitele 2, 3, 4, 6, 8, 12, 16, 18, 24 a číslo 75 má dělitele 3, 5, 15, 25; součet 2 + 3 + 4 + 6 + 8 + 12 + 16 + 24 = 75 a 3 + 5 + 15 + 25 = 48). Další speciální skupina čísel souvisejících s děliteli jsou čísla původní. Tak se označují čísla, která nelze vyjádřit jako součet dělitelů některého jiného čísla (např. číslo 22 není původní, protože ho můžeme zapsat jakou sečet dělitelů čísla 38). Původní čísla jsou 2, 5, 52, 88 a 96.
Jestliže součet dělitelů daného čísla (kromě jeho samého) je větší než číslo samo, pak se nazývá abundantní. Příkladem takového čísla je třeba 70 (1 + 2 + 5 + 7 + 10 + 14 + 35 = 74, což je víc než 70). Zvláštním případem abundantního čísla je číslo výstřední. To je takové, které nelze získat jako součet některých jeho dělitelů. Takových čísel je velmi málo a jediným takovým číslem menším než sto je číslo 70. Pokud je součet dělitelů čísla (kromě jeho samého) menší než ono číslo, pak se nazývá deficientní. Příkladem deficientního čísla je třeba číslo 26 (1 + 2 + 13 = 16, což je méně než 26). Prvočísla jsou extrémně deficientní, protože součet jejich dělitelů je vždy 1. Jako nedosažitelné číslo se označuje číslo, které není součtem dělitelů žádného čísla. Příkladem je dvojka.
Pokud číslo není ani abundantní, ani deficientní, tj. součet jeho dělitelů (kromě jeho samého) dává součet přesně ono číslo, pak se toto číslo nazývá dokonalé. Nejnižším takovým číslem je 6, neboť 1 + 2 + 3 = 6, další jsou například 28 (1 + 2 + 4 + 7 + 14), 496 (1 + 2 + 4 + 8 + 16 + 31 + 62 + 124 + 248), 8 128 a další už leží za hranicí milionu. Lze dokázat, že všechna dokonalá čísla končí buď číslicí 6 nebo dvojčíslicí 28 (to jsou zároveň první dvě dokonalá čísla). Prvních pět dokonalých čísel bylo známo již v 16. století, ale dodnes nevíme, zda existuje největší dokonalé číslo nebo zda pokračují do nekonečna. Dokonalá čísla jsou předmětem zkoumání, neboť zatím není jasná řada souvislostí. Může být dokonalé číslo liché? Asi ne, zatím nebylo žádné takové nalezeno, ale chybí důkaz. Existuje číslo, jehož součet dělitelů je o jedničku větší než číslo samotné? Opět - takové nebylo nalezeno. K hledání dokonalých čísel lze použít výsledky práce Eukleida a Leonharda Eulera. N je sudé dokonalé číslo, jestliže n = 2p – 1 (2p - 1), kde 2p - 1 je Mersennovo prvočíslo (těch je v současnosti známo necelých padesát).
Pokud najdeme všechny prvočíselné dělitele, můžeme každé přirozené číslo zapsat s použitím mocnin jako tzv. prvočíselný rozklad. Např. číslo 41 184 = 25 · 32 · 111 · 131. Tento zápis je jednoznačný, tzn. že neexistuje zápis stejného čísla pomocí jiných prvočísel. Tato jednoznačnost se nazývá základní věta aritmetiky.
Pokud máme dvě a více čísel rozložených na dělitele, pak můžeme určit společný násobek a dělitel, popř. největší společný dělitel a nejmenší společný násobek. Pro kontrolu platí pro největší společný dělitel a nejmenší společný násobek dvou čísel a, b
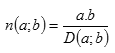
Přirozená čísla nazýváme soudělná, jestliže mají alespoň jednoho společného dělitele většího než jedna. V opačném případě, tj. když je největší společný dělitel jen jedna, říkáme, že čísla jsou nesoudělná.
K nalezení největšího společného dělitele a nejmenšího společného násobu můžeme využít prvočíselný rozklad obou čísel. Největší společný dělitel má ve svém prvočíselném rozkladu všechny společné prvočinitele rozkladů obou čísel s nejmenším mocnitelem, který se v těchto rozkladech vyskytuje. Nejmenší společný násobek má ve svém prvočíselném rozkladu každého z prvočinitelů rozkladů obou čísel s největším mocnitelem, který se v těchto rozkladech vyskytuje.
Eukleidův algoritmus hledání největšího společného dělitele větších čísel vysvětlíme na příkladu. Najděme největšího společného dělitele čísel 116 a 36. Využijeme poznatku, že největší společný dělitel dvou čísel dělí také jejich rozdíl. Na základě tohoto poznatku budeme postupovat. 116 – 36 = 80, budeme tedy hledat největší společný dělitel čísla 36 a 80. To jsou ale stále dost velká čísla. Proto je opět odečteme 80 – 36 = 44. Hledáme největší společný dělitel čísel 36 a 44. I teď si situaci zjednodušíme odečtením 44 – 36 = 8. Hledáme největší společný dělitel čísel 8 a 36. Pokračujeme stejně dál 36 – 8 = 28. Hledáme největší společného dělitele čísel 28 a 8. Pokračujeme stejně dál 28 – 8 = 20. Hledáme největší společný dělitel 20 a 8. Pokračujeme stejně dál 20 – 8 = 12. Hledáme největší společný dělitel čísel 12 a 8 a to je na první pohled číslo 4, což je i hledaný největší dělitel čísel 116 a 36.
Použité zdroje:
[1] CRILLY, T. Matematika. 50 myšlenek, které musíte znát. 1. vydání. Praha: Slovart, 2010. ISBN: 978-80-7391-409-7.
[2] SPENCER, A. Kniha čísel. 1. vydání. Praha: Albatros, 2005. ISBN: 13-805-KMČ-005.
[3] ZIEGLER, G. Matematika vám to spočítá. Příběhy královny věd. Praha: Knižní klub, 2011. ISBN 978-80-242-3311-6.
