Již od pradávna se lidé snažili si ulehčit aritmetické výpočty. Pomoc přišla až se zavedením pozičních soustav a rozvojem různých mechanických pomůcek. Nejstarším prapředkem počítače je kuličkové počítadlo abakus a mechanismus z Antikythéry, který byl vyroben mezi lety 150 – 100 před n. l.
Abakus
Abakus patří mezi první a nejdéle používanou počtářskou pomůcku, která pokrokově používala desítkovou soustavu. Pochází pravděpodobně z Babylónu z doby 2700 – 2300 před n. l. Předchůdce abaku byly tzv. počítací desky, které se používaly kolem roku 1000 před n. l. Ty měly podobu soustavy rýh, po kterých se posouvaly drobné předměty – kamínky, zrníčka apod. Později byly desky vyráběné ze dřeva, a proto nejstarším dochovaným abakem je Salamínská tabule vyrobená z mramoru, která pochází z doby cca 300 let před n. l. (byla objevená na ostrově Salamis).
Desky byly postupně nahrazeny rámem, ve kterém byly rovnoběžně na drátcích navlečené korálky (kaménky, kuličky), které se po drátcích mohly volně pohybovat. Zruční počtáři s touto pomůckou nejenom sčítali a odčítali, ale také násobili, dělili a počítali druhé a třetí odmocniny. Postupně vzniklo několik variant abaku. Kolem roku 1200 vznikla v Číně varianta označovaná jako 2/5, která se používá dodnes. O tři sta let později vznikla v Japonsku varianta 1/4.
Japonská varianta 1/4 se skládá z řady kovových tyčinek, které jsou pomocí lišty rozděleny na menší horní díl a větší spodní díl. V horní části se nachází vždy po jednom dřevěném korálku, ve spodní vždy po čtyřech korálcích. Tyčinka úplně napravo představuje jednotky. Ta bezprostředně vedle ní nalevo představuje desítky, další stovky atd. Korálky ve spodní polovině mají hodnotu 1, ty v horní polovině hodnotu 5. Korálky se počítají tehdy, když jsou blízko lišty, která dělí tyčinky na dvě poloviny, tedy když jsou přisunuty ke středu. Chceme-li nastavit určité číslo, posuneme nejdříve odpovídající počet korálků představujících jednotky ke střední liště. Když nestačí 4, přidá se horní korálek představující 5.
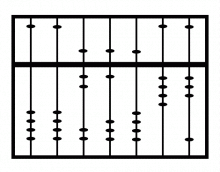
Abakus s nastaveným číslem 76 543.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.
Při sčítání nebo odčítání přidáváme/odebíráme korálky po jedné na místě jednotek, desítek atd. Pokud při sčítání jdeme přes desítku (např. 17 + 8), pak součet převedeme na 17 + 10 – 2.
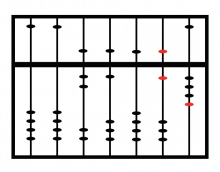
Abakus s nastaveným výpočtem 76 543 + 21.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.
Při násobení (např. 28 ∙ 3) nejprve vynásobíme desítky (20 ∙ 3 = 60) a pak jednotky (8 ∙ 3 = 24) a ty pak sečteme. Pokud násobíme víceciferným číslem (např. 25 ∙ 12), pak nejprve vynásobíme jednotkami (25 ∙ 2, to rozdělíme na 20 ∙ 2 a 5 ∙ 2) a pak desítkami (25 ∙ 10, to rozdělíme na 10 ∙ 2 a 10 ∙ 5).
Čínská varianta 2/5 se skládá z řady kovových tyčinek, které jsou pomocí lišty rozděleny na menší horní díl a větší spodní díl. V horní části se nachází vždy dva dřevěné korálky, ve spodní vždy pět korálků. Tyčinka úplně napravo představuje jednotky. Ta bezprostředně vedle ní nalevo představuje desítky, další stovky atd. Korálky ve spodní polovině mají hodnotu 1, ty v horní polovině hodnotu 5. Korálky se počítají tehdy, když jsou blízko lišty, která dělí tyčinky na dvě poloviny, tedy když jsou přisunuty ke středu.
Chceme-li nastavit určité číslo, posuneme nejdříve odpovídající počet korálků představujících jednotky ke střední liště. Když nestačí 4, přidá se horní korálek představující 5.
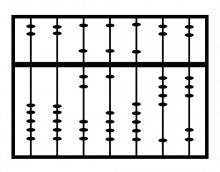
Abakus s nastaveným číslem 76 543.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.
Jednotlivé početní úkony provádíme podobně jako u verze 1/4.
Mechanické stroje
V průběhu 16. století se podstatně zvýšily nároky na matematické výpočty. Do té doby používané početní algoritmy byly těžkopádné a zdlouhavé a počtáři dělali mnoho chyb. Jednou z cest bylo nahradit násobení jinou operací nebo odstranit psaní pomocných výpočtů. To realizoval John Napier svými tyčkami. Ve své knize O rabdologii neboli o počítání s tyčkami z roku 1617 ukázal, že všechny násobky malé násobilky, které se používají v algoritmu gelosia, lze předem napsat na proužky papíru a z nich pak složit pravoúhelníkovou tabulku potřebnou k výpočtu součinu daných čísel. Napier ještě navrhl zlepšení spočívající v tom, že se proužky nalepí na čtyři stěny kvádru a vzniknou tak tyčka (bacilli Neperianes). Napierovy tyčky vzbudily větší ohlas než jeho logaritmické tabulky. Bylo s nimi možné nejen násobit, dělit ale i počítat druhé odmocniny.
Průkopníkem mezi vynálezci mechanických počítacích strojů byl Wilhelm Schickard, který v roce 1623 vynalezl počítací hodiny, které sčítaly, odčítaly, násobily a dělily. Popis jeho vynálezu byl objeven až po jeho smrti a připravil o prvenství Blaise Pascala, který v roce 1642 sestrojil pascalínu, osmimístný sčítací stroj, který měl sloužit jeho otci ke zpracování velkého množství dat. V roce 1670 se Wilhelm Leibniz pokusil sestrojit strojek s přímým mechanickým násobením a dělením. O dva roky později si podle svého návrhu nechal sestrojit model a o rok později ho chtěl předvést před členy Royal Society, ale strojek nefungoval. Až o rok později se Leibnizovi podařil rozhodující objev posuvných stupňovitých ozubených válečků, s nimiž lze provádět přesné přičítání či odčítání v daném řádu a při spojení s dalším mechanismem lze zajistit automatický převod do řádu vyššího (či nižšího). Ke konečné variantě svého stroje – Leibnizova kola - dospěl Leibniz až v roce 1694 a zlepšoval ho dalších šestnáct let. Na základě principu Leibnizova stroje vyráběl Ch. X. Thomas aritmometr sériově.
Leibniz měl další následníky: Wilgodta Odhnera, který zkonstruoval aritmometr podle návrhu Giovanniho Poleniho; Jacoba Leopolda, Phillipa Hahna nebo Charlese Babbage, který který zkonstruoval diferenční stroj a analytický stroj. K řízení druhého použil děrné štítky.
Logaritmické pravítko
Počítání s logaritmickými tabulkami vedlo velmi brzy k myšlence přenést logaritmickou stupnici na pravítko a využít jeho posouvání. V roce 1620 s touto myšlenkou vystoupil Edmund Gunter, pracoval však s kružidly při přenášení délek. Ideu dvou pohyblivých logaritmických stupnic přinesl snad už William Oughtred, ale publikoval ji až v roce 1632, navrhl také stupnice na okrajích soustředných kruhů. Průhledného jezdce navrhl prý Isaac Newton v 17. století, ale zaveden byl až o sto let později. Současnou podobu dostalo logaritmické pravítko až v 19. století u A. Mannheima.
Logaritmické pravítko se skládá ze tří částí: pravítka, posouvátka a běhounu s vyritou čárou. Logaritmické pravítko se používalo k výpočtu druhých mocnin a odmocnin, někdy i třetích, k násobení a dělení a podle vybavení pravítka i k dalším výpočtům. Logaritmické pravítko je vybaveno jednou normální stupnicí a několika logaritmickými stupnicemi. Ty se vyznačují tím, že vzdálenost jednotlivých dílků se se vzrůstajícím číslem zmenšuje. Posouváním jezdce nebo posouvátka se pak provádějí jednotlivé početní operace.
Kalkulačky
Konstruktéři kalkulaček nebo také kapesních výpočetních pomůcek se často inspirovali v konstrukcích mechanických strojů popsaných v předchozí kapitole. Zajímavou mechanickou pomůckou je Consul the Educated Monkey, který byl patentován 27. června 1916 Williamem Robertsonem.
Dalším zajímavým mechanismem je Darnleyho kalkulátor patentovaný roku 1920. Jedná se o pouzdro na psací potřeby tvořené dvěma souosými válci s různými průměry. Na vnitřním válci je umístěna multiplikační tabulka, z níž je viditelné pouze záhlaví řádků. Záhlaví sloupců je na otočném, vnějším válci, s otvory v příslušném sloupci. Rotací otočné části lze nastavit vedle sebe dvojici násobených činitelů a součin se pak objeví v otvoru vedle nich.
Další skupinu tvoří kapesní sčítací strojky, které byly ve své době levné a hlavně přenosné. Jejich tělo je zpravidla rozděleno na dvě části – jedna pro sčítání a jedna pro odčítání, uprostřed jsou umístěna výsledková okénka. Výpočet se provádí posouváním pohyblivých částí jen na základě jednoduchého algoritmu. Příkladem můžem být Rychlopočtář od firmy Znak, který se vyráběl v 50. a 60. letech minulého století nebo Produx M, Efzeta nebo Tarema z německé produkce.
Na principu pascalíny pracují addometery, které na rozdíl od předchozích kalkulaček mají přechod přes desítku zajištěný automaticky pomocí převodů ozubených kol. Addometery se vyráběly v letech 1928 až 1950.
V padesátých letech minulého století začal vývoj elektronických kalkulaček. Vznikl ale problém se vzrůstajícím počtem součástek a tím i s finanční náročností výroby a nebezpečím poruch. Jack Kilby si v roce 1964 patentoval první integrovaný obvod s jediným tranzistorem. Kvůli vysoké ceně výrobek nešel na odbyt. Nakonec firma Texas Instruments, pro kterou Kilby pracoval, přišla v roce 1969 s kapesním elektronickým kalkulátorem s integrovaným obvodem, který uměl sčítat, odčítat, násobit a dělit. První vědecká kalkulačka byla uvedena na trh v roce 1972, programovatelná kalkulačka TI-58 se objevila v roce 1976 a ve stejném roce se začaly používat LCD displeje, které umožnily grafický výstup.
Elektronické počítače
První elektromagnetický reléový počítač sestrojil v roce 1938 Konrad Zuse, označil ho Z1 a navázal na něj počítači Z2 a Z4. V roce 1944 sestrojil Howard Aiken ve spolupráci s firmou IBM počítač Harvard MARK 1, který měl reléovou paměť. Počítač měřil téměř 16 metrů a vážil 4,5 tuny. Na něj navázaly další tři počítače Harvard Mark II. – IV. Tyto počítače jsou označovány jako nultá generace.
První elektronický počítač byl sestrojen v roce 1946 pod vedením Johna Mauchlyho a Johna Prespera Eckerta ve spolupráci s Johnem von Neumannem. Dostal název ENIAC (Elektronic Numerical Integrator and Computer). Zabíral plochu 167 m2, vážil 27 tun, skládal se z 17 468 elektronek a vykonával 5000 aritmetických operací za sekundu. Během druhé světové války používala tento počítač americká armáda, pak byl použit při vývoji termojadernné bomby. Tímto počítačem začíná éra tzv. počítačů první generace (jejich charakteristickým znakem je, že pracovaly pomocí elektronek). Počítač ENIAC se stal inspirací pro poíčtač MANIAC (Mathematical Analyser Numerical Integrator and Computer), který postavil John von Neumann v roce 1945. Prvním komerčně vyráběným počítačem byl UNIVAC (UNIVersal Automatic Computer) z roku 1951. Vyrobilo se 46 kusů.
Druhá generace počítačů využívala tranzistory a první takový počítač vznikl v roce 1953 pod vedením Toma Kulburna na University of Manchester. Třetí generace počítačů využívala integrované obvody a první takový počítač vznikl v roce 1964. V současnosti se vyrábějí počítače čtvrté generace, které používají mikroprocesory. Prvním počítačem čtvrté generace byl osobní počítač IBM PC 5150, který byl uveden na trh 12. srpna 1981.
Použité zdroje:
[1] BEUTELSPACHER, A. Matematika do vesty. Praha: Baronet a. s., 2005. ISBN 80-7214-841-9.
[2] POMP, M. – VÁCLAVÍKOVÁ, Z. Historie kapesních výpočetních pomůcek. 32. mezinárodní konference Historie matematiky. Praha: matfyzpress, 2011, s. 237-240. ISBN 978-80-7378-128-6.
[3] PORUBSKÁ, E. – LAMOŠ, F. Matematika 8 pro střední odborné školy a studijní obory středních odborných učilišť. Praha: Státní pedagogické nakladatelství, 1986. ISBN 14-627-86.
[4] PRECLÍK, J. Abakus. Rozhledy matematicko–fyzikální, roč. 77, č. 4, s. 168-175. ISSN 0035-9343.
[5] RYŠAVÝ, V. O počítacích strojích. Časopis pro pěstování mathematiky a fysiky, 1927, roč. 56, s. 90–106.
[6] VÁCLAVÍKOVÁ, Z. Historické výpočetní pomůcky a netradiční metody aritmetických výpočtů. 31. mezinárodní konference Historie matematiky. Praha: matfyzpress, 2010, s. 275-278. ISBN 978-80-7378-128-6.
[7] Encyklopedická edice, listy, matematici. ISBN 80–860–44–05–X.