S rovnoměrným přímočarým pohybem se v praxi setkáme poměrně zřídka (např. při jízdě na dálnici). Častěji se setkáme s pohybem, při kterém se rychlost mění. Takový pohyb nazýváme nerovnoměrný. Zrychlený pohyb je pohyb, při kterém se rychlost hmotného bodu, popř. tělesa, neustále zvětšuje, popř. zmenšuje (rovnoměrně zpomalený pohyb). Pokud je přírůstek rychlosti za sekundu stále stejný, jde o rovnoměrně zrychlený pohyb.
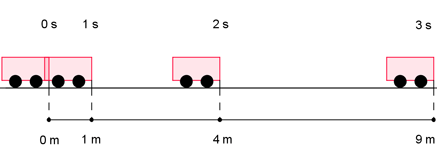
Zrychlený pohyb.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.
Když Galileo Galilei řešil problém, jak popsat změnu rychlosti pohybujícího se tělesa, navrhl změnu rychlosti za jednotku času. Chtěl totiž popsat "přirozeně zrychlený" pohyb (volný pád) a byl intuitivně hluboce přesvědčen, že volný pád je rovnoměrně zrychlený právě v tomto smyslu a nikoliv ve smyslu změny rychlosti připadající na délkovou jednotku dráhy. Kdybychom tuto jeho myšlenku zapsali dnešním způsobem, pak
![]()
kde Δ označuje změnu nebo také přírůstek rychlosti rovnoměrně zrychleného pohybu, tj. rozdíl mezi konečnou rychlostí v2 a počáteční rychlostí v1, tedy Δv = v2 − v1. Vztah platí jen za předpokladu, že se rychlost rovnoměrně zvyšuje po celou dobu Δt. Veličina, kterou jsme označili a, byla později nazvána zrychlení (accelaratio). Dosazením do definičního vztahu získáme jednotku
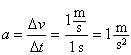
tedy metr za sekundu na druhou (m s–2).
Zrychlení má směr vektoru rychlosti. Jestliže má již hmotný bod nějakou počáteční rychlost v0, pak vztah pro rychlost můžeme přepsat do tvaru
![]()
a graficky znázornit

Grafická závislost rychlosti na čase u rovnoměrně zrychleného pohybu.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.
Při rovnoměrně zpomaleném pohybu se velikost rychlosti rovnoměrně zmenšuje s časem, zrychlení má opačný směr než rychlost. Je–li v0 počáteční rychlost hmotného bodu, je velikost jeho okamžité rychlosti v čase t dána vztahem
![]()
a grafické znázornění
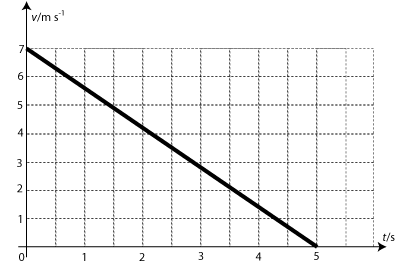
Grafická závislost rychlosti na čase u rovnoměrně zpomaleného pohybu.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.
K odvození závislosti dráhy na čase využil Galileo Galilei tzv. Galileiho padostroj. Bylo to prkno 7,2 m dlouhé. V něm byl vyhlouben žlábek a byl potažen hladkým pergamenem. Do žlábku zapadla bronzová koule. Čas měřil množstvím vody vyteklé z velkého vodou naplněného sudu. Srovnáním množství vody a délky, po které koule padala, objevil závislost dráhy na druhé mocnině času. Pokusy spadají do let 1602 až 1604 a vyšly v roce 1638 v Discorsi dimostrazioni matematice … (Rozpravy o dvou nových oborech vědních). Současným zápisem můžeme jeho závislost zapsat
![]()
kde s je dráha, a zrychlení a t doba rovnoměrně zrychleného pohybu, který začal z klidu. Tuto závislost můžeme vyjádřit graficky
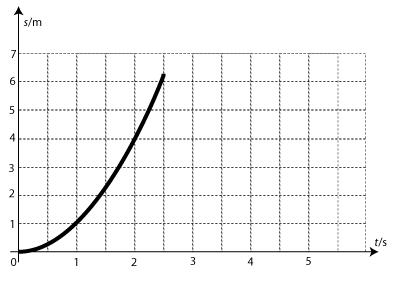
Grafická závislost dráhy na čase u rovnoměrně zpomaleného pohybu.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.
Výpočtem pak dostaneme dobu t v závislosti na dráze s.
![]()
Jestliže těleso má již nějakou počáteční rychlost vo a pohybuje se zrychleně/zpomaleně, pak pro výpočet dráhy použijeme vztah
![]()
Lidské tělo nedokáže vnímat rychlost. Příkladem může být jízda v autě rychlostí 90 km h–1 a v letadle rychlostí 900 km h–1. Naše tělo si pohyb vůbec neuvědomuje. Pokud by však náhle auto či letadlo začalo měnit svou rychlost, pociťujeme tuto změnu velmi intenzivně až nepříjemně. Vzpomeňte si na rozjíždění a zastavování výtahu.
