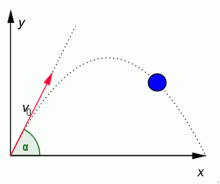
Ve sportu i ve vojenské technice má velký význam šikmý vrh. Koná ho těleso, kterému udělíme počáteční rychlost v0 ve směru, který svírá s vodorovnou rovinou úhel α. Úhel α se nazývá elevační úhel. Pohyb tělesa můžeme rozložit na rovnoměrný přímočarý pohyb šikmo vzhůru počáteční rychlostí v0 a volný pád ve svislém směru.
Šikmý vrh.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.
Výsledným pohybem šikmého vrhu je parabola, jejíž vrchol je v nejvyšším bodě trajektorie. Zakreslíme–li trajektorii šikmého vrhu do souřadnicové soustavy, můžeme popsat jeho pohyb pomocí rovnic
Rovnici dráhy hmotného bodu v soustavě souřadnic v rovině dostaneme, když z obou rovnic vyloučíme parametr t
Koeficienty při x a x2 jsou konstanty, a proto je daná rovnice rovnicí paraboly se svislou osou.
Když těleso dopadne, můžeme určit délku vrhu d, po dosazení y = 0 a po úpravě dostáváme
Evangelista Torricelli v roce 1644 zjistil, že délka vrhu závisí na počáteční rychlosti a na elevačním úhlu. Dostřel je stejný pro úhel α i pro úhel 90o – α. Maximální délka vrhu (dostřel) je při úhlu 45o. Tato hodnota dělí křivky na dvě skupiny: ploché (využívají je kanony, kulomety, pušky a pistole) a strmé (minomety).
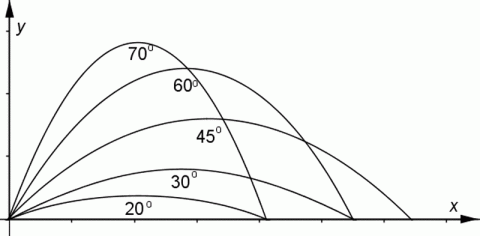
Závislost dostřelu na elevačním úhlu.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.
Odpor vzduchu mění trajektorii šikmého vrhu na balistickou křivku. Kam má mířit střelec – to znázorňuje animace.
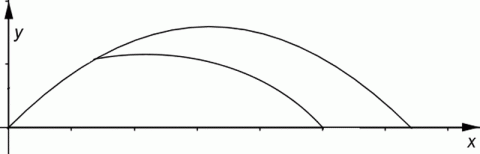
Balistická křivka.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.
Použité zdroje:
[1] VYBÍRAL, V. Balistická křivka. Fyzika ve škole, červen 1968, roč. 6, č. 10. s. 433–441.
