Věda a technika v pozadí
Keplerovy zákony
Zdroj: Techmania Science Center. Autor: Pavel Trnka. Under Creative Commons.
Teorie
První Keplerův zákon pochází z roku 1605 a společně s druhým zákonem byl publikován v Astronomia nova o čtyři roky později:
Planety obíhají kolem Slunce po elipsách málo odlišných od kružnic, v jejichž společném ohnisku je Slunce.
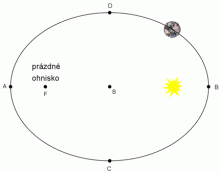
První Keplerův zákon.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.
Vrchol elipsy B, v němž je planeta Slunci nejblíže, se nazývá perihélium neboli přísluní. Vrchol A, v němž je planeta od Slunce nejdále, se nazývá afélium neboli odsluní.
První Keplerův zákon hovoří o elipse. Ta patří mezi kuželosečky společně s hyperbolou a parabolou. Mezi základní charakteristiky každé kuželosečky patří lineární excentricita nebo-li výstřednost. Ta u elipsy představuje vzdálenost ohniska od středu kuželosečky. V astronomii se používá numerická excentricita (číselná výstřednost), která je vyjádřená poměrem lineární excentricity a délky hlavní poloosy. Vyjadřuje relativní velikost odchylky dráhy tělesa od dokonalé kružnice. Podle hodnoty excentricity můžeme rozlišit tvar dráhy.
| e = 0 | kružnice |
| 0 < e < 1 | elipsa |
| e = 1 | parabola |
| e > 1 | hyperbola |
Jak ale vypadá ta zemská elipsa? Numerická excentricita zemské dráhy je 0,017, lineární excentricita je 2,5, tedy velmi malé číslo. Proto se dráha Země velmi málo liší od kružnice (na náčrtku ji můžeme kružnicí nahradit, protože rozdíl hlavní a vedlejší poloosy na našem obrázku je mm, vzdálenost Slunce v ohnisku od středu elipsy řádově desetiny milimetru). Skutečná dráha Země je ale daleko větší, proto vzdálenost Slunce od středu elipsy je téměř 2,5 milionů km. V porovnání se vzdáleností Slunce – Země je to nepatrné číslo.
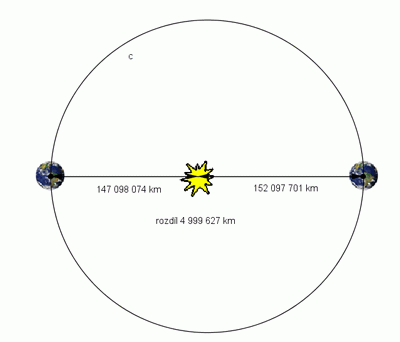
Zemská elipsa.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.
Jak jsou na tom s excentricitou jiná tělesa sluneční soustavy?
| těleso | numerická excentricita | tvar dráhy |
|---|---|---|
| planetka Schlaun | 0,002 | téměř kružnice |
| Venuše | 0,007 | téměř kružnice |
| Neptun | 0,011 | elipsa |
| Země | 0,017 | elipsa |
| Uran | 0,047 | elipsa |
| Jupiter | 0,048 | elipsa |
| Saturn | 0,054 | elipsa |
| Mars | 0,093 | elipsa |
| Merkur | 0,205 | elipsa |
| Halleyova kometa | 0,967 | téměř parabola |
| kometa Hyakutake | 0,9998 | téměř parabola |
| kometa McNaught | 1,00001 | hyperbola |
| kometa C/1980 E1 | 1,057 | hyperbola |
Druhý Keplerův zákon:
Plošné obsahy opsané průvodičem planety za jednotku času jsou konstantní.
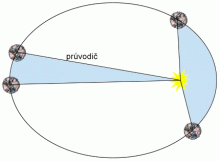
Druhý Keplerův zákon.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.
Průvodič planety je úsečka spojující střed planety se středem Slunce. Při pohybu se délka a směr průvodiče neustále mění, ale obsahy ploch, které průvodič opíše za stejné doby jsou stejné. Nejkratší průvodič má planeta v perihéliu a nejdelší v aféliu. V důsledku toho je rychlost planety v perihéliu větší než v aféliu – animace. Tato skutečnost společně se sklonem roviny ekliptiky (rovina ekliptiky je rovina ve které obíhá Země kolem Slunce) k rovníku způsobují, že slunečné dny nejsou na Zemi během roku stejně dlouhé, a proto musíme používat střední sluneční čas. Na severní polokouli Země trvá letní půlrok 186 dní, zatím co zimní půlrok 179 dní. Země je v perihéliu počátkem ledna, v aféliu počátkem července.
Třetí Keplerův zákon pochází z roku 1618 a publikován byl ve spise Harmonices mundi libri quinque, geometricu, architectonicus, harmonicus, psychologicus, astronomicus cum appendice continens mystérium cosmographicum o rok později:
Poměr druhých mocnin oběžných dob dvou planet se rovná poměru třetích mocnin délek hlavních poloos jejich trajektorií.
Označíme–li T1, T2 oběžné doby dvou planet, a1, a2 délky hlavních poloos, pak třetí Keplerův zákon vyjádříme vztahem
![]()
Tento zákon platí za předpokladu, že hmotnosti planet jsou zanedbatelně malé vzhledem k hmotnosti Slunce, což je u planet sluneční soustavy splněno, neboť hmotnost největší planety Jupitera je jen jedna tisícina hmotnosti Slunce. Jako srovnávací planeta se většinou používá Země. Proto byla zavedena nová délková jednotka, která představuje střední vzdálenost Země od Slunce – astronomická jednotka se zkratkou AU (1 AU = 1,496 · 108 km).
Keplerovy zákony platí nejen pro pohyby planet, ale obecně pro každou soustavu těles, která se pohybují v centrálním gravitačním poli tělesa, jehož hmotnost je mnohonásobně větší než hmotnost těles obíhajících. Platí proto také pro soustavu umělých družic Země, či Jupiterovy měsíce.


