S pojmem mocnina se setkáváme už u starověkých Řeků při řešení geometrických úloh. Obsah čtverce, objem krychle a podobné problémy měření vedly k vytvoření pojmů druhé a třetí mocniny. Kroky vedoucí k vytvoření pojmů vyšších mocnin nebyly tak snadné. Nejprve bylo třeba odpoutat se od geometrické představy, která se spojovala s každým aritmetickým výkonem. Přesto se o čtvrté mocnině hovoří už u Herona z Alexandrie. Diofantos z Alexandrie uvádí možnost zápisu šesté mocniny, ale používá pouze třetí mocniny při řešení rovnic. Velký vliv na rozvoj pojmu mocniny a počítání s mocninami měly indické poznatky, které přinesl do Evropy Musa al-Chvárizmí a jiní. Trvalo však ještě velmi dlouho, než nauka o mocninách dosáhla své dnešní podoby. Nynější zápis mocnin ve tvaru an = a · a · a ·…· a, kde a se násobí celkem n-krát (n je celé číslo a a je reálné číslo) zavedl ve svém díle Géométire René Descartes. Číslo a se nazývá základ mocniny nebo mocněnec, číslo n exponent nebo mocnitel. Jako symbol druhé odmocniny se před rokem 1400 používalo přeškrtnuté velké písmeno R (ze slova radix – kořen). Symbol √ představuje zkomolené písmeno R. Poprvé se tento symbol objevil ve spisu Coss z roku 1525 od Christoffa Rudolffa. Běžně se začal objevovat v matematických spisech až během několika následujících století. Pro libovolné přirozené číslo n definovat n-tou odmocninu z nezáporného čísla a jako takové nezáporné číslo b, pro něž platí bn = a, označujeme b = n√a. Číslo a se nazývá základ odmocniny nebo odmocněnec, číslo n odmocnitel.
O mocninách čísel byla zjištěna řada zajímavostí:
- jako automorfní číslo se označuje takové číslo, jehož druhá mocnina končí na to stejné číslo, např. 762 = 5776
- druhou mocninu kteréhokoli lichého čísla většího než jedna můžeme zapsat jako násobek osmi zvětšený o jedna, např. 52 = 3 ∙ 8 +1
- podobně součin čtyř po sobě jdoucích čísel zvětšený o jednu představuje druhou mocninu některého čísla, např. 1 ∙ 2 ∙ 3 ∙ 4 +1 =25, 6 ∙ 7 ∙ 8 ∙ 9 +1 = 3025 = 552
- zajímavé hodnoty druhých mocnin mají čísla tvořená samými jedničkami: 12 = 1, 112 = 121, 1112 = 12 321, 111 111 1112 = 12 345 678 987 654 321
- zajímavé druhé mocniny mají čísla tvořená jednou sedmičkou a několika šestkami: 72 = 49, 672 = 4 489, 6672 = 444 889, 6 6672 = 44 448 889, …
- zajímavé jsou také některé součty mocnin: 102 + 112 + 122 = 132 + 142, 33 + 43 + 53 = 63
Výpočet druhé mocniny a odmocniny
Druhou mocninu můžeme vypočítat pomocí vztahu (a + b)2 = a2 + 2ab + b2, např. 462 = (40 + 6)2 = 402 + 2 ∙ 40 ∙ 6 + 62 = 1600 + 480 + 36 =2116 nebo 692 = (70 – 1)2 = 702 – 2 ∙ 70 ∙ 1 +12 = 4900 – 140 + 1 = 4761. Podobně bychom mohli vypočítat kteroukoli další mocninu pomocí binomické věty
![]() 0
0
Při výpočtu druhé mocniny větších čísel můžeme použít následující algoritmus:
- vypočítáme druhou mocninu první číslice
- k dvojnásobku čísla zapsaného první číslicí připíšeme druhou číslici a vzniklé číslo násobíme touto druhou číslicí,
- k dvojnásobku čísla zapsaného prvními dvěmi číslicemi připíšeme třetí číslici a vzniklé číslo násobíme třetí číslicí,
- dále pokračujeme v načatém algoritmu,
- součin každého dalšího řádku píšeme o dvě místa vpravo.
Starořečtí matematikové používali pravděpodobně k výpočtu druhé odmocniny přibližnou hodnotu podle vzorce
![]()
Tento způsob odmocňování znali prý už Babyloňané.
V Čínském spisu Matematika v devíti knihách z přelomu letopočtu je uveden historicky nestarší popis výpočtu druhé i třetí odmocniny. Číňané při výpočtu používali čínskou verzi abaku.
I když se v současnosti spoléháme při výpočtu druhé odmocniny na kalkulačku, bylo donedávna běžné ji spočítat na papíře jen s pomocí násobení a odečítání. Při výpočtu druhé odmocniny postupujeme podle tohoto algoritmu:
- odmocněnce rozdělíme na dvojčísli zprava doleva, při desetinném čísle na dvojčísli od desetinné čárky doprava i doleva
- první číslici odmocniny dostaneme odmocněním prvního dvojčíslí
- od prvního dvojčíslí odečteme druhou mocninu první číslice odmocniny a k rozdílu připíšeme další dvojčíslí
- v dělenci zatrhneme poslední místo a zbylé číslo dělíme dvojnásobkem dosavadního výsledku,
- výsledek dělení zapíšeme do výsledku a současně ho připíšeme k děliteli
- vzniklé číslo násobíme stejným číslem a výsledek odečteme od původního čísla (viz příklad).
Existuje několik metod přibližného výpočtu druhé odmocniny. Postup jedné z nich si ukážeme na příkladu výpočtu √30. Výsledek dokážeme odhadnout, bude to 5 a nějaké desetiny k tomu. Můžeme to tedy zapsat
![]()
Pokud určujeme jen přibližnou hodnotu, tak x2 můžeme zanedbat, protože se jedná o mocninu desetinného čísla, jejíž hodnota je malá. Pak platí
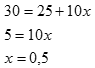
Odmocnina z třiceti je v prvním přiblížení 5,5. Pokud budeme chtít výsledek přesnější, zaměníme v předchozím výpočtu 5 za 5,5, tedy
![]()
x2 můžeme zanedbat, pak platí
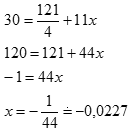
Při druhém přiblížení dostáváme hodnotu 5,5 - 0,0227 = 5,4773, která se od té skutečné liší až na čtvrtém desetinném místě.
Použité zdroje:
[1] BEUTELSPACHER, A. Matematika do vesty. Praha: Baronet, 2005. ISBN 80-7214-841-9.
[2] MOLNÁR, J. – MACHAČÍKOVÁ, I. Co z historie matematiky do vyučování? Sborník Dva dny s didaktikou matematiky 2011.
[3] PERELMAN, J. I. Zajímavá geometrie. Praha: Mladá Fronta, 1954.
[4] PORUBSKÝ, Š. Dokonalé čísla. Najstarší otvorený problém matematiky. 29. mezinárodní konference Historie matematiky, Velké Meziříčí, 22. 8. – 26. 8. 2008, s. 33–48 1. vydání. Praha: Matfyzpress, 2008. ISBN 978-80-7378-048-7.
[5] SPENCER, A. Kniha čísel. 1. vydání. Praha: Albatros, 2005. ISBN: 13-805-KMČ-005.
[6] STEWART, I. Truhlice matematických pokladů profesora Stewarta. Praha: Dokořán, 2013. ISBN 978-80-7363-527-5.
[7] ŠEDIVÝ, O. Matematika pro 8. ročník základní školy 1. díl. 1. vydání. Praha: Státní pedagogické nakladatelství, 1991. ISBN 80-04-25091-2.
[8] Encyklopedická edice, listy, matematici. ISBN 80–860–44–05–X.


