Řešit úlohu eukleidovsky znamená použít pouze pravítko a kružítko. Existuje několik úloh, které jsou známé už od dob starého Řecka a nejdou eukleidovsky vyřešit. Důkaz o tomto tvrzení ale přišel až v 19. století třeba od Lva Landaua nebo Jánose Bolyaie. Jsou to úlohy s názvem kvadratura kruhu, trisekce úhlu, reduplikace krychle, rektifikace kružnice a cirkularita kruhu. Všechny úlohy mají jedno společné – snaží se narýsovat iracionální číslo.
Kvadratura kruhu spočívá v narýsování čtverce, jehož obsah se přesně rovná obsahu daného kruhu. Řada matematiků se problémem zabývala – např. Johann Lambert, Adrien Legendre, Charles Hermite – ale bez většího úspěchu. Důvodem je iracionalita čísla π. Můžeme ale najít přibližné řešení této úlohy, které je naznačeno na obrázku.
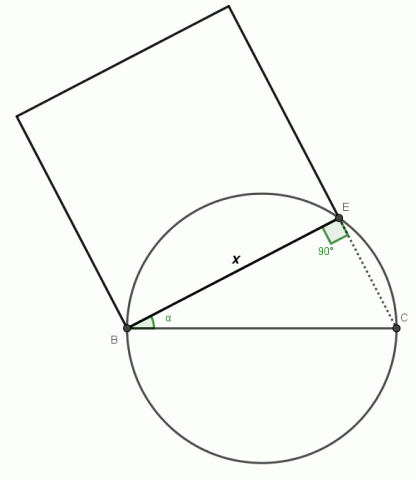
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.
Hledaná velikost strany čtverec odpovídá velikosti úsečky BE. K tomu potřebujeme vypočítat velikost úhlu α. Z trigonometrie platí, že
![]()
Strana hledaného čtverce je pak x = 2r cos α, obsah takového čtverce x2 = 4r2 cos2α. Obsah čtverce ale musí být stejný jako obsah kruhu πr2.
![]()
A odtud pro úhel α = 27°36´.
Pokud narýsujeme v daném kruhu tětivu pod úhlem 27°36´ k průměru, dostaneme přímo stranu čtverce, který bude mít stejný obsah jako kružnice.
Opačnou úlohou je cirkularita kruhu. Úkolem je sestrojit úsečku, která je poloměrem kruhu, který má stejný obsah jako daný čtverec.
Trisekce úhlu spočívá v rozdělení libovolného úhlu na tři stejné díly. Důkaz, že trisekci nelze provést pravítkem a kružítkem, podal v roce 1837 Pierre Wantzel pomocí algebraických metod. Opět lze úlohu vyřešit přibližně. Kolem vrcholu úhlu A opíšeme libovolnou kružnici a příslušnou tětivu prodloužíme o dvě třetiny její délky. Z takto nalezeného bodu P narýsujeme kružnici o poloměru rovném velikosti tětivy. Tato kružnice protne daný oblouk přibližně ve třetině.
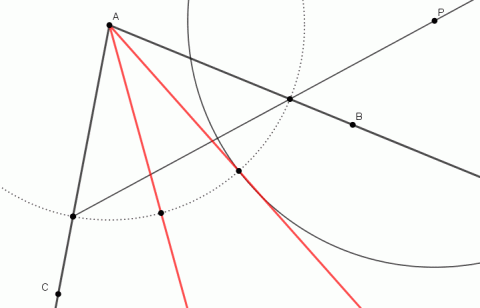
Přibližná metoda konstrukce trisekce úhlu.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.
Duplikace krychle je konstrukce úsečky, která je hranou krychle s dvojnásobným objemem než je objem dané krychle. Problémem je sestrojení třetí odmocniny ze dvou. Tato úloha je známá pod názvem Delfská úloha. Podle pověsti obyvatelé řeckého města Athény poslali do známé věštírny v Delfách svého posla, aby od věštce získali radu, jak ukončit řádění moru. Bylo jim řečeno, že musí postavit nový oltář, který bude mít objem rovný dvojnásobku objemu stávajícího oltáře. Později zkonstruoval Eratosthenes pomůcku, kterou tuto úlohu mohl vyřešit. Mezi dvě rovnoběžné kolejničky je napevno umístěný jeden pravoúhlý trojúhelník (červený) a dva pohyblivé trojúhelníky, které jsou s ním totožné (šedé). Na pevném trojúhelníku je střed strany K. Pohyblivé trojúhelníky nastavíme tak, jak ukazuje obrázek – aby přímka procházející bodem K procházela i ostatními body na obrázku. Pokud je DK hrana krychle, pak ML je hrana krychle s dvojnásobným objemem.
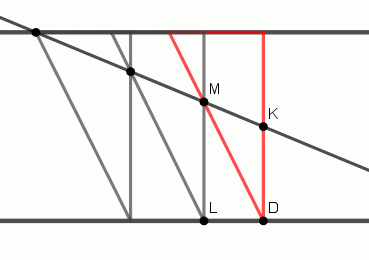
Eratosthenova pomůcka ke konstrukci duplikace krychle.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.
Rektifikace kružnice spočívá v narýsování obvodu kružnice. Problémem je sestrojení čísla π. Existuje několik přibližných konstrukcí, např. Kochaňského konstrukce.
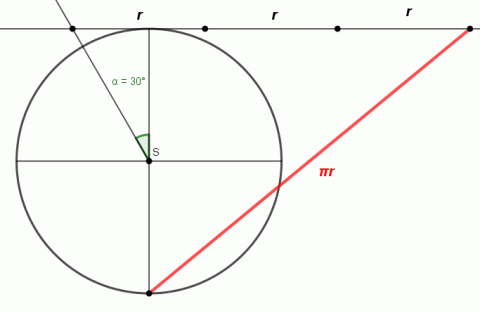
Kochaňského konstrukce rektifikace kružnice.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.
Použité zdroje:
[1] CRILLY, T. Matematika. 50 myšlenek, které musíte znát. 1. vydání. Praha: Slovart, 2010. ISBN: 978-80-7391-409-7.
[2] PERELMAN, J. I. Zajímavá geometrie. Praha: Mladá Fronta, 1954.
[3] STEWART, I. Kabinet matematických kuriozit profesora Stewarta. Praha: Dokořán, 2013. ISBN 978-80-7363-292-2.
[4] TARABY, O. Příspěvek ku trisekci úhlu. Časopis pro pěstování mathematiky a fysiky, 1906, roč. 35, s. 76–77.
