Teorie
Chaotické kyvadlo ukazuje, jak jednoduché zatočení kolečka, má za následek nepředvídatelný a komplikovaný pohyb. Chaotické kyvadlo představuje fyzikální systém, který je citlivý na počáteční podmínky. V důsledku citlivosti systému na počáteční podmínky se chování takového fyzikálního systému jeví jako náhodné.
Jednoduché kyvadlo kmitá pravidelně, pokud mu nedodáváme energii, tak i tlumeně. Jiná situace nastane, pokud kyvadlo doplníme otočným kloubem. Kmitání kyvadla se stane naprosto chaotickým, nepředvídatelným.
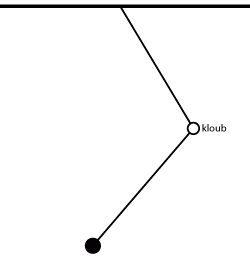
Kyvadlo doplněné otočným kloubem.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.
Rozvoj teorie chaosu přišel až s prvními počítači (jeden z prvních byl ENIAC, který předpovídal počasí). Teorie chaosu se dá aplikovat na dráhy kulečníkových koulí, golfových míčků, problém více těles – například soustavu dvanácti Neptunových měsíců.
V roce 1961 se Edward Lorenz zabýval numerickými simulacemi počasí. Pracoval v MIT (Massachusetts Institute of Technology) a jeho stařičký počítač měl za úkol vykreslit zajímavý graf počasí. Trvalo mu to dlouho, a tak si Lorenz zašel na kávu. Když přišel, tak byl hodně překvapený. Graf vypadal úplně jinak než předešlý den. Myslel si, že zadal počáteční podmínky stejně, ale pak zjistil, že v předchozím grafu zadal hodnoty na šest desetinných míst a teď na tři. Aby vysvětlil tyto nesrovnalosti, musel zavést pojem „efekt motýlího křídla“. Ten znamená, že nepatrná vzdušná turbulence se může přeměnit v hurikán na druhé straně zeměkoule - nepatrné změny počátečních podmínek mohou vést k dalekosáhlým změnám systému.
Lorenz se problémem zabýval podrobněji a zjistil, že vývoj počasí z různých počátečních pomínek vede jen k určitým koncovým stavům. Tyto koncové stavy nazval atraktory. Koncové stavy nelze zpětným dopočtem určit. Pokud velmi málo odlišné počáteční podmínky vedou k úplně jiným výsledkům, nazýváme takový atraktor podivný. Nejznámější je Lorenzův podivný atraktor.
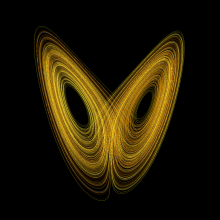
Lorenzův podivný atraktor.
Zdroj: commons.wikimedia.org. Public domain.
Teorie chaosu vznikla přibližně ve stejné době jako teorie fraktálů. Obě teorie mají k sobě blízko, například některé podivné atraktory jeví fraktální strukturu.




