Z historie
Tribar se poprvé objevil v roce 1934 v díle švédského umělce Reutersvärda. Jeho dílo ale zůstalo prakticky až do 80. let 20. století neznámé. V roce 1954 Roger Penrose spolu se svým otcem Lionelem publikoval článek o „nemožných tvarech“. Tento článek poslal nizozemskému grafikovi Mauritsi Escherovi, který do svých dalších děl zakomponoval dva Penroseovy nemožné tvary – Penroseův trojúhelník a Penroseovo schodiště.
Penroseův trojúhelník a Penroseovo schodiště.
Zdroj: commons.wikimedia.org. Public domain.
Teorie
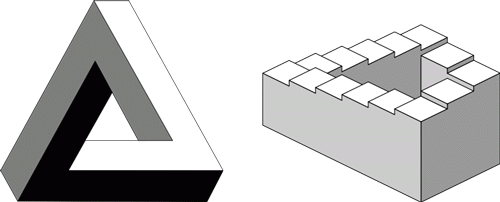
Podivný trojúhelník je zajímavý objekt, který se při pohledu z určitého místa jeví jako tzv. Penroseův trojúhelník. Při jiném pohledu tato iluze zaniká a je vidět skutečný tvar objektu, který nemá s tribarem nic společného. Penroseův trojúhelník ukazuje tři trámy, které jsou vzájemně spojené v pravých úhlech a přesto tvoří trojúhelník. Tím samozřejmě porušují několik zákonů euklidovské geometrie. Mezi jinými i zákon, který říká, že součet úhlů v každém trojúhelníků je 180°. Penroseův trojúhelník se skládá z jednotlivých dílů, které jsou bezpochyby správné, jejich existence je možná. Jednotlivé díly jsou spojené takovým způsobem, který je možný pouze na dvojrozměrné ploše obrazu, nikoliv však v reálném trojrozměrném světě.
Podivný trojúhelník patří mezi psychologické klamy. Ke vzniku těchto iluzí dochází převážně při pozorování rovinných předloh, které svou konfigurací mají vyjadřovat průmět trojrozměrného prostoru a jimž tuto prostorovou povahu vědomě či mimovolně přisuzujeme. Příčinou vzniku těchto klamů jsou čistě psychologické důvody.
Na otázku, jak je nemožný tribar možný, dal Roger Penrose jednoduchou odpověď: "Nemožný objekt vzniká jako důsledek nesprávného spojení jednotlivých dílů. Vzniká tak klamný dojem existence nemožného."
Roger Penrose přišel ještě s jednou geometrickou zajímavostí, tzv. Penroseovou mozaikou. V roce 1974 vytvořil rovinnou mozaiku z více než jednoho druhu dlaždic – kosočtverce, jejiž úhly jsou 36° a 144° u jednoho a 72° a 108° u druhého. Kosočtverce se sestavují v mozaiku podle určitých pravidel. Podíl počtu větších a menších kosočtverců je v nekonečné Penrosově teselaci roven přesně zlatému řezu. Toto číslo je iracionální, a proto v Penroseově mozaice nelze definovat jedinou elementární buňku.
Penrosova mozaika.
Zdroj: commons.wikimedia.org. Under Creative Commons.Za deset let byla objevena i fyzikální aplikace v krystalografii. Jako první přišel se souvislostí Penrosovy mozaiky a kvazikrystalů Alan MacKay v roce 1981. V roce 1984 Peter Kramer a Reinhardt Neri a nezávisle na nich Dov Levine a Paul Steinhardt zkonstruovali třírozměrné analogon Penroseovy mozaiky, které má velmi úzký vztah ke struktuře kvazikrystalů. Třírozměrná Penrosova mozaika jeví ikosaedrickou symetrii a pravidelné uspořádání. Základními stavebními jednotkami jsou dva klence neboli romboedry (tělesa omezená šesti kosočtverečnými stěnami). Vnitřní úhly v romboedrech jsou stejné jako úhly, které spolu svírají určité vazby v ikosaedrických atomech. Podíl počtu romboedrů jednoho a druhého druhu v nekonečné třírozměrné Penroseově mozaice je roven zlatému řezu. Způsob, jakým by podle výpočtů Penrosova mozaika rozptylovala záření, jeví pozoruhodnou shodu s experimentálními výsledky získanými difrakcí na kvazikrystalech.
