Název geometrie znamenal původně zeměměřičství (geo = země, metrein = měřit). Měřit zemi začali lidé velmi dávno, snad v Egyptě, Mezopotámii, Indii, Číně nebo v jiné vzdělané kultuře. Tak třeba ve starověkém Egyptě. Řeka Nil pravidelným střídáním období záplav a sucha sužovala její obyvatele, kteří museli každý rok znovu a znovu vyměřovat svá políčka. Proto se rozhodli stavět zavlažovací kanály, zpočátku primitivní, ale postupem času je začali vyměřovat a objevovat základní geometrická pravidla. Nyní je geometrie chápána jako část matematiky, která se zabývá studiem geometrických objektů. Její součástí je planimetrie, která studuje geometrické útvary v rovině, a stereometrie, která studuje geometrické útvary v prostoru.
Mezi nejstarší doklady o rýsování patří ovál, který vytesali do kvádrového zdiva stavitelé chrámu v egyptském Luxoru asi 1200 let před n. l. Šířka oválu je více než jeden a půl metru. Rýsování do kamene se dříve často používalo a pomůže nám dnes v některých případech poznat již zmizelé památky. Příkladem je půdorys na základové dlažbě chrámu v Egyptě na ostrově Filé, jehož zdivo bylo již v dávných dobách rozebráno. Rozvoj rýsování byl v minulosti většinou spojen s rozvojem stavitelství. Při vyměřování základů staveb se používaly tyče a provazce.
Velké znalosti z geometrie trojúhelníku měli již více než půl tisíciletí před naším letopočtem staří Řekové. Mnohé poznatky přejímali od starších kulturních národů, zejména Egypťanů. Získané poznatky však značně obohatili. Jejich zásluhou se geometrická tvrzení snad poprvé v historii dokazovala. Z bohaté historie geometrie vyberme jen jeden problém, který začíná ve 4. století před n. l. u Eukleida. Ten napsal tu nejdůležitější knihu o geometrii, která se skládá ze 13 knih a jmenuje se Základy. Zde Eukleides logicky vybudoval s pomocí pěti axiomů, řady definic, obecných pojmů, vět a jejich důkazů model geometrie. I když soustava není úplná, přesto tato kniha dlouhá léta sloužila jako učebnice geometrie. Na anglických školách byla používána ještě v minulém století. Pět Eukleidových axiomů:
- Lze spojit jeden bod s druhým přímkou.
- Každá úsečka může být prodloužena spojitě na přímku.
- Kružnici lze popsat bodem a vzdáleností.
- Všechny pravé úhly jsou si rovny.
- Jestliže přímka se dvěma dalšími přímkami vytváří na stejné straně vnitřní úhly s velikostí menší než dva pravé úhly, pak ať je umístěna kdekoliv, vždy tyto přímky protne na té straně, na níž jsou úhly menší než dva pravé úhly.
Na první pohled je vidět, že pátý axiom se odlišuje od všech ostatních. Euklides s ním nebyl spokojen a pokoušel se mu co nejdéle vyhnout. Proto prvních 28 vět dokázal bez jeho použití.
Na konci 19. století matematici poprvé připustili, že Eukleides vycházel z nevyslovených domněnek. Velkou polemiku vyvolal jeho pátý axiom. Na první pohled je vidět jeho délka, těžkopádný styl a rozvleklost. I sám Eukleides s jeho formulací spokojený nebyl, ale potřeboval ho k důkazu dalších tvrzení. V roce 1795 jej John Plyfair upravil do této podoby: „Je-li dána přímka l a bod P neležící na této přímce, pak existuje jediná přímka, která prochází bodem P a je rovnoběžná s přímkou l.“ Přibližně ve stejné době přišel Adrien Legendre s další rovnocennou formulací, ve které tvrdil, že součet úhlů v trojúhelníku se rovná 180°.
Ani snaha dokázat pátý axiom nebyla úspěšná. O důkaz se pokusila celá řada matematiků. Všichni pracovali vždy s úmyslem ho dokázat, protože věřili, že jeho existence je nezbytná. Mezi řadou neznámých jmen jako John Wallis, Girolamo Saccheri byla i řada matematických osobností jako Johann Lambert nebo Adrien Legendre. Zajímavá je Saccheriho práce. K důkazu přistoupil obráceně. Použil první čtyři postuláty a místo pátého vzal tvrzení, které odporuje pátému axiomu a logickou cestou chtěl přijít ke sporu. To se ale nestalo. Logickou cestou odvodil řadu pouček, které však byly v rozporu s eukleidovskou geometrií. Nakonec se přiklonil k nevědeckému řešení a prohlásil, že jeho důkaz je falešný, protože odporuje přirozenosti přímky.
Nový pohled na věc přinesla až práce Carla Gausse, Jánose Bolyaie a Nikolaje Lobačevského. Ti k pátému axiomu přistupovali jinak. Snažili se jeho existenci naopak popřít. Gauss práci nezveřejnil, i když k ní dospěl už v roce 1817. Zřejmě ve strachu z reakce matematiků. Lobačevsky své výsledky publikoval v roce 1829 a nezávislý na něm o dva roky později dospěl ke stejným výsledkům i Bolyai. Dokázali, že pátý axiom je na předchozích nezávisí a že připojením jeho negace k předchozím čtyřem vznikne nová geometrie. Bolyai a Lobačevsky zvolili pátý axiom tak, že povolili daným bodem vést více než jednu přímky, které by neprotínaly danou přímku. Jak je to možné? Třeba tehdy, když novou geometrii budeme pěstovat na zakřivené ploše. Příkladem může být hyperbolická plocha, kde součet úhlů v trojúhelníku je menší než 180° a navíc součet úhlů závisí na velikosti trojúhelníku (čím větší trojúhelník, tím menší součet). Lobačevskij ve své geometrii odvodil řadu trigonometrických identit a ukázal, že v malých rozměrech se tyto identity blíží k běžným identitám euklidovského prostoru.
Lobačevského geometrie byla zpočátku odmítána jako nesmyslná teorie. Pomohlo jí až sestrojení několika eukleidovských modelů, ve kterých platí zásady této geometrie. Takovým modelem je Poincarého kruhový model.
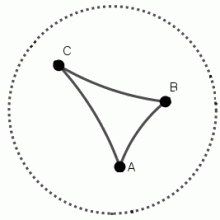
Trojúhelník ABC znázorněný v Poincarého kruhovém modelu Lobačevského geometrie.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.
Na práci Lobačevského a Bolyaie navázal v 50. letech 19. století Bernhard Riemann, který přeformuloval druhý axiom na „všechny přímky mají konečnou délku, ale nemají žádný konec“. Zároveň upravil axiom o rovnoběžkách tak, že neexistuje přímka procházející bodem, která je rovnoběžná s danou přímkou. Jedním z modelů této geometrie je koule. Úlohu přímek tu hrají hlavní kružnice (se středem ve středu koule). V této geometrii, kterou nazýváme eliptická, je součet vnitřních úhlů trojúhelníku větší než 180° a také závisí na velikosti trojúhelníku (čím větší trojúhelník, tím větší součet).
Použité zdroje:
[1] CRILLY, T. Matematika. 50 myšlenek, které musíte znát. 1. vydání. Praha: Slovart, 2010. ISBN: 978-80-7391-409-7.
[2] CRILLY, T. Velké otázky. Matematika. Praha: Knižní klub, 2012. 1. vydání. ISBN: 978-80-242-3596-7.
[3] HAVLÍČEK, K. Sté výročí smrti Jánose Bolyaie. Pokroky matematiky, fyziky a astronomie, roč. 5 (1960), č. 3, s. 345-357.
[4] MACHÁČEK, M. S Cabri do tajů lobačevského geometrie. Učitel matematiky, 2008, roč. 16, č. 3 (67), s. 160–170. ISSN 1210–9037.

