Teorie
Apollónios z Pergy je autorem osmisvazkového díla Kuželosečky. První čtyři knihy se dochovaly v řečtině, další tři v arabském překladu a poslední se ztratila. Apollóniův přístup ke kuželosečkám se neobvykle velkou všeobecností odlišuje od metod všech jeho předchůdců. Zatímco do Apollónia se každý z třech druhů kuželoseček získával z různých druhů kruhových kuželů, Apollónius je všechny získával z libovolného kruhového kuželu bez ohledu na to, či je přímý nebo kosý. Jako první zavedl dodnes používané pojmenování pro kuželosečky: elipsa, parabola a hyperbola. Apollóniova metoda předstihla metodu analytické geometrie. Objevují se v ní první náznaky souřadnicového systému.
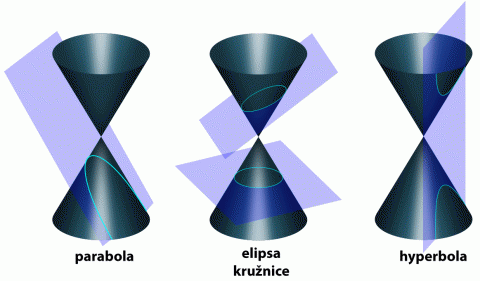
Všechny známé kuželosečky můžeme vyrobit řezáním kuželu. Představte si dva kužele spojené ve vrcholu, které jsou nekonečné. Jestliže budeme kužel řezat rovinou kolmou na osu kužele, dostaneme kružnici. Když tuto rovinu trošku nakloníme, řezem bude elipsa. Při dalším naklánění roviny se nám řez náhle "otevře", dostali jsme parabolu. Stačí jen malé vychýlení roviny a řez bude dvojdílný, protože rovina v této poloze protne oba dva kužele. Řezem je tentokrát hyperbola.
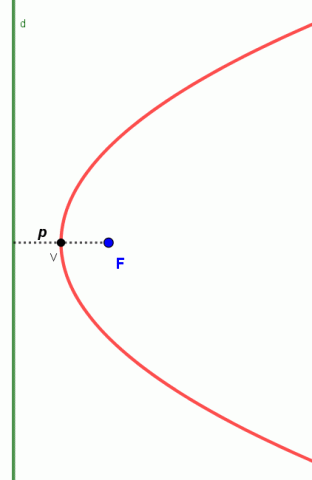
Podívejme se podrobně na parabolu. Parabola je množina všech bodů roviny, které mají stejnou vzdálenost od bodu F a dané přímky d, která tímto bodem neprochází. Bod F se nazývá ohnisko a přímka d se nazývá řídící přímka. Základní charakteristikou paraboly je parametr p, který představuje vzdálenost ohniska a řídící přímky.
Základní charakteristiky elipsy.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.
Tvar paraboly má dráha družice opouštějící Zemi 2. kosmickou rychlostí, dráha tělesa vrženého šikmo vzhůru (neuvažujeme-li odpor vzduchu), řez reflektorem, zrcadlem dalekohledu.
Dvě paraboly se společnou osou mají zajímavou vlastnost: pokud vyšleme zvuk nebo světlo z ohniska, tak se vždy odrazí rovnoběžně s osou paraboly. Pokud zvuk nebo světlo narazí na parabolu druhou, pak se odrazí do jejího ohniska. Proto si dva lidé stojící každý v ohnisku jedné paraboly mohou i na větší vzdálenost povídat.
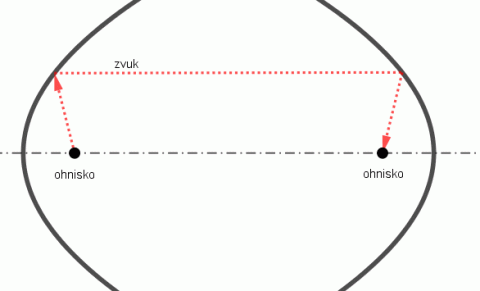
Odraz zvuku v exponátu.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.
Podobnou vlastnost jako dva paraboloidy v exponátu, má i elipsoid. Zvuk jdoucí z jednoho ohniska se odráží do druhého ohniska.

Odraz zvuku v elipsoidu (jeho průmět do jedné roviny).
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.
Proto např. v kostele, kde strop má tvar přibližně části elipsoidu mohli mniši v dobách inkvizice odposlouchávat cizí tiché hovory, aniž by si toho kdokoli všiml. Původním záměrem takto postavených kostelů byla dobrá slyšitelnost kněze ve všech částech kostela. Kromě toho srozumitelnosti přispívá tzv. „gregoriánský chorál“, jehož pravidla vycházejí z přirozené řeči. Daný jev můžeme pozorovat na vhodně tvarovaných stěnách např. v chrámu sv. Pavla v Londýně, v divadle v Mohuči, v sále karyatid v Louvru v Paříži apod. Obdobný tvar má i kukaň nápovědy v divadle.