Kyvadlem může být každé tuhé těleso otáčivé kolem vodorovné osy umístěné nad jeho těžištěm, takové kyvadlo nazýváme fyzické. Kmitavý pohyb kyvadel, které mají různý tvar a hmotnost, je poměrně složitý. Proto zavedeme jednoduchý model kyvadla, kterým je matematické kyvadlo, jehož závěs je nehmotný. Přibližně ho realizujeme zavěšením malé těžší kuličky na tenkou pevnou nit, jejíž hmotnost je zanedbatelně malá vzhledem k hmotnosti kuličky. Pro frekvenci f a periodu kmitání T matematického kyvadla můžeme odvodit

kde l je délka kyvadla a g tíhové zrychlení. Frekvence a perioda harmonického pohybu matematického kyvadla závisí na délce jeho závěsu a na velikosti tíhového zrychlení v daném místě.
Kmitavý pohyb můžeme považovat za harmonický přibližně jen v krátkém časovém úseku. Po delším pozorování zjišťujeme, že amplituda kmitů se s časem zmenšuje až nakonec kmity zaniknou. Podobně jako u jiných pohybů projeví se působení odporových sil. Kmitání, které by probíhalo neomezeně dlouho beze změn své amplitudy, se nazývá kmitání netlumené. Ze zkušenosti však víme, že amplituda výchylky mnohých kmitavých pohybů se postupně zmenšuje, až kmitání zanikne. Probíhá kmitání tlumené.
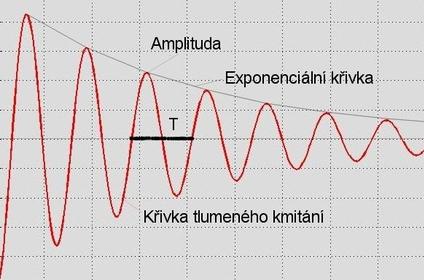
Amplituda tlumeného kmitání.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.
Příčinou tlumeného kmitání jsou síly, které vznikají v samotném oscilátoru (při deformaci pružných částí oscilátoru) nebo při styku s prostředím (odporová síla prostředí). V obou případech se část mechanické energie oscilátoru postupně mění ve vnitřní energii oscilátoru a prostředí, čímž se oscilátor i prostředí v jeho nejbližším okolí zahřívá. Kromě amplitudy se zmenšuje i perioda kmitání.
Kdybychom kmitající kuličku ponořili do různých prostředí, tak může dojít k aperiodickému přetlumenému pohybu (těleso nepřejde přes rovnovážnou polohu), kriticky tlumenému aperiodickému pohybu (těleso dojde do rovnovážné polohy) a tlumenému periodickému kmitavému pohybu. Tlumením se omezují nepříznivé účinky kmitavých pohybů, např. kol automobilů při jízdě na nerovném terénu – tlumiče pérování, ruček měřících přístrojů apod.
Frekvence a perioda kmitán kyvadla nezávisí na hmotnosti kyvadla ani na jeho rozkyvu (jen pokud je úhel rozkyvu malý). Tato myšlenka je už velmi stará, své počátky má snad už v Číně, ve starém Řecku, u Mikuláše z Oresme, Leonarda da Vinci, Girolama Cardana a dalších. První vědecký popis se objevil někdy v roce 1583 nebo 1584 od Galilea Galilei, ten na tuto závislost přišel pravděpodobně při pozorování lustrů v pisánském chrámu během bohoslužeb, ale bohužel se ve svých výpočtech mýlil. Správný výsledek zveřejnil až v roce 1687 Isaac Newton. Zákonitost ověřil při pokusu se stejně dlouhými kyvadly, jejichž duté kuličky byly z různých látek, ale měly stejný objem (aby byl odpor vzduchu stále stejný). Všechna kyvadla se kývala stejně. Při malých rozkyvech nezávisí doba kyvu na velikosti rozkmitu. Mezi další pokračovatele patřil Christian Huygens, Leonhard Euler, Simeon Poisson, Adrien Legendre nebo Carl Jacobi.


Galileo Galilei a Isaac Newton.
Zdroj: Techmania Science Center. Autor: Pavel Trnka. Under Creative Commons.





